(本小题满分14分)
设函数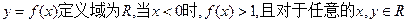 ,有
,有 。
。
(1)求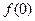 的值;(2)求数列
的值;(2)求数列 的通项公式;(3)是否存在正数
的通项公式;(3)是否存在正数 均成立,若存在,求出k的最大值,并证明,否则说明理由。
均成立,若存在,求出k的最大值,并证明,否则说明理由。
(本小题满分14分)已知函数f(x)=(1+x)lnx.
(1)求函数f(x)在x=1处的切线方程;
(2)设g(x)= ,对任意x∈(0,1),都有g(x)<-2,求实数a的取值范围;
,对任意x∈(0,1),都有g(x)<-2,求实数a的取值范围;
(本小题满分13分)已知椭圆C: (a>b>0)的两个焦点分别为F1(-
(a>b>0)的两个焦点分别为F1(- ,0)、F2(
,0)、F2( ,0).点M(1,0)与椭圆短轴的两个端点的连线相互垂直.
,0).点M(1,0)与椭圆短轴的两个端点的连线相互垂直.
(1)求椭圆C的方程;
(2)过点M(1,0)的直线l与椭圆C相交于A、B两点,设点N(3,2),记直线AN、BN的斜率分别为k1、k2,求证k1+k2为定值.
(本小题满分12分)已知等差数列{an}的前n项和为Sn=n2+pn+q(p,q∈R),且a2,a3,a5成等比数列
(1)求p,q的值;
(2)若数列{bn}满足an+log2n=log2bn,求数列{bn}的前n项和Tn.
(本小题满分12分)为了宣传今年10月在我是举办的“第十五届中国西部博览会”组委会举办了“西博会”知识有奖问答活动,随机对市民15~65岁的人群抽样n人,回答问题统计结果如下图表所示:
(1)分别求出a,x的值;
(2)从地2,3,4组回答正确的人中用分层抽样的方法抽取6人,“西博会”组委会决定在所抽取的6人中随机抽取2人颁发幸运奖,求所抽取的人中第2组至少有1人获得幸运奖的概率.
(本小题满分12分)如图,在四棱柱ABCD-A1B1C1D1中,侧面ADD1A1⊥底面ABCD,D1A=DD1=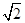 ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2.
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2.
(1)求证:A1O∥平面AB1C;
(2)求三棱锥B1-ABC的体积.