(本小题满分12分)为了宣传今年10月在我是举办的“第十五届中国西部博览会”组委会举办了“西博会”知识有奖问答活动,随机对市民15~65岁的人群抽样n人,回答问题统计结果如下图表所示:
(1)分别求出a,x的值;
(2)从地2,3,4组回答正确的人中用分层抽样的方法抽取6人,“西博会”组委会决定在所抽取的6人中随机抽取2人颁发幸运奖,求所抽取的人中第2组至少有1人获得幸运奖的概率.
已知各项均为正数的数列{an}前n项和为Sn,首项为2,且2,an,Sn成等差数列。
|
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若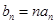 ,求数列
,求数列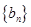 的前n项和Tn.
的前n项和Tn.
在非等腰△ABC中,a,b,c分别是三个内角A,B,C的对边,且a=3,c=4,C=2A.
(Ⅰ)求cosA及b的值;
(Ⅱ)求cos(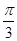 –2A)的值.
–2A)的值.
天津医专在2015年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下图所示.
(1)请先求出频率分布表中①、②位置相应数据,再在答题纸上完成下列频率分布直方图;
(2)为了能选拔出最优秀的学生,学校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受李医生进行面试,求:第4组至少有一名学生被李医生面试的概率?
| 组号 |
分组 |
频数 |
频率 |
| 第1组 |
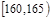 |
5 |
0.050 |
| 第2组 |
 |
① |
0.350 |
| 第3组 |
 |
30 |
② |
| 第4组 |
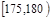 |
20 |
0.200 |
| 第5组 |
 |
10 |
0.100[ |
| 合计 |
100 |
1.00 |
在△ABC中,若A=120°,AB=5,BC=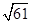 ,
,
(1)求AC边长及sinB;
(2)求△ABC的面积S.
编号为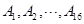 的16名篮球运动员在某次训练比赛中的得分记录如下:
的16名篮球运动员在某次训练比赛中的得分记录如下:
| 运动员编号 |
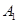 |
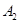 |
 |
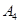 |
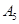 |
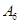 |
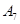 |
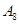 |
| 得分 |
15 |
35 |
21 |
28 |
25 |
36 |
18 |
34 |
| 运动员编号 |
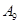 |
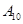 |
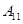 |
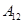 |
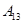 |
 |
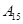 |
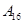 |
| 得分 |
17 |
26 |
25 |
33 |
22 |
12 |
31 |
38 |
(Ⅰ)将得分在对应区间内的人数填入相应的空格;
| 区间 |
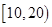 |
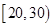 |
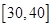 |
| 人数 |
(Ⅱ)从得分在区间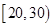 内的运动员中随机抽取2人,
内的运动员中随机抽取2人,
(i)用运动员的编号列出所有可能的抽取结果;
(ii)求这2人得分之和大于50的概率.