已知在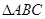 中,D是AB上一点,
中,D是AB上一点, 的外接圆交BC于E,
的外接圆交BC于E, .
.
(Ⅰ)求证: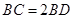 ;
;
(Ⅱ)若CD平分 ,且
,且 ,求BD的长.
,求BD的长.
已知 ,
,
(Ⅰ)当 时,若
时,若 在
在 上为减函数,
上为减函数, 在
在 上是增函数,求
上是增函数,求 值;
值;
(Ⅱ)对任意 恒成立,求
恒成立,求 的取值范围.
的取值范围.
椭圆 过点
过点 ,离心率为
,离心率为 ,左、右焦点分别为
,左、右焦点分别为 ,过
,过 的直线交椭圆于
的直线交椭圆于 两点.
两点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)当 的面积为
的面积为 时,求直线的方程.
时,求直线的方程.
生产 ,
,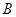 两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
| 测试指标 |
 |
 |
 |
 |
 |
元件 |
8 |
12 |
40 |
32 |
8 |
元件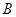 |
7 |
18 |
40 |
29 |
6 |
(Ⅰ)试分别估计元件 、元件
、元件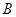 为正品的概率;
为正品的概率;
(Ⅱ)生产一件元件 ,若是正品可盈利50元,若是次品则亏损10元;生产一件元件
,若是正品可盈利50元,若是次品则亏损10元;生产一件元件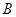 ,若是正品可盈利100元,若是次品则亏损20元,在(Ⅰ)的前提下
,若是正品可盈利100元,若是次品则亏损20元,在(Ⅰ)的前提下
(i)求生产5件元件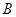 所获得的利润不少于300元的概率;
所获得的利润不少于300元的概率;
(ii)记 为生产1件元件
为生产1件元件 和1件元件
和1件元件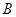 所得的总利润,求随机变量
所得的总利润,求随机变量 的分布列和期望.
的分布列和期望.
如图,四棱锥 中,底面ABCD为菱形,
中,底面ABCD为菱形, ,Q是AD的中点.
,Q是AD的中点.
(Ⅰ)若 ,求证:平面PQB
,求证:平面PQB 平面PAD;
平面PAD;
(Ⅱ)若平面APD 平面ABCD,且
平面ABCD,且 ,点M在线段PC上,试确定点M的位置,使二面角
,点M在线段PC上,试确定点M的位置,使二面角 的大小为
的大小为 ,并求出
,并求出 的值.
的值.