一个袋中有若干个大小相同的黑球、白球和红球。已知从袋中任意摸出1个球,得到黑球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是
.
(Ⅰ)若袋中共有10个球,
(i)求白球的个数;
(ii)从袋中任意摸出3个球,记得到白球的个数为
,求随机变量
的数学期望
.
(Ⅱ)求证:从袋中任意摸出2个球,至少得到1个黑球的概率不大于
。并指出袋中哪种颜色的球个数最少.
选修4—5;不等式选讲.
设函数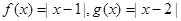 .
.
(Ⅰ)解不等式 ;
;
(Ⅱ)对于实数 ,若
,若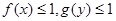 ,求证
,求证 .
.
选修4—4;坐标系与参数方程.
已知直线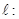
 为参数), 曲线
为参数), 曲线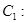
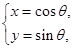 (
( 为参数).
为参数).
(Ⅰ)设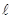 与
与 相交于
相交于 两点,求
两点,求 ;
;
(Ⅱ)若把曲线 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的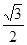 倍,得到曲线
倍,得到曲线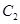 ,设点
,设点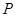 是曲线
是曲线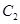 上的一个动点,求它到直线
上的一个动点,求它到直线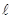 的距离的最小值.
的距离的最小值.
选修4—1:几何证明选讲
如图,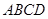 是圆的内接四边形,
是圆的内接四边形, ,过
,过 点的圆的切线与
点的圆的切线与 的延长线交于
的延长线交于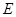 点,证明:
点,证明:
(Ⅰ)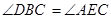 ;
;
(Ⅱ) .
.
已知函数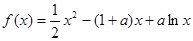 ,其中
,其中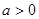 .
.
(Ⅰ) 求函数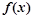 的极小值点;
的极小值点;
(Ⅱ)若曲线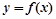 在点
在点 处的切线都与
处的切线都与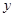 轴垂直,问是否存在常数
轴垂直,问是否存在常数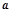 ,使函数
,使函数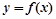 在区间
在区间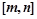 上存在零点?如果存在,求
上存在零点?如果存在,求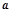 的值:如果不存在,请说明理由.
的值:如果不存在,请说明理由.
平面内与两定点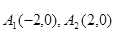 连线的斜率之积等于非零常数
连线的斜率之积等于非零常数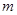 的点的轨迹,加上
的点的轨迹,加上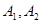 两点,所成的曲线
两点,所成的曲线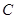 可以是圆,椭圆或双曲线.
可以是圆,椭圆或双曲线.
(I)求曲线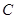 的方程,并讨论
的方程,并讨论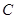 的形状与
的形状与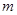 值的关系.
值的关系.
(Ⅱ)当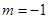 时,对应的曲线为
时,对应的曲线为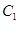 ;对给定的
;对给定的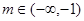 ,对应的曲线为
,对应的曲线为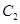 ,若曲线
,若曲线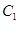 的斜率为
的斜率为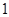 的切线与曲线
的切线与曲线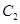 相交于
相交于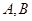 两点,且
两点,且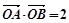 (
(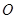 为坐标原点),求曲线
为坐标原点),求曲线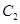 的方程.
的方程.