某人抛掷一枚质量分布均匀的骰子,出现各数的概率都是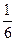 ,构造数列
,构造数列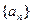 ,使
,使
 ,记
,记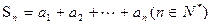 .
.
(Ⅰ)求 时的概率;
时的概率;
(Ⅱ)求前两次均为奇数且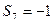 的概率.
的概率.
(本小题满分13分)在△ABC中,a、b、c分别是角A、B、C的对边,且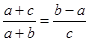 ,
,
(1)求角B的大小;
(2)若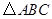 最大边的边长为
最大边的边长为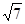 ,且
,且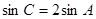 ,求最小边长.
,求最小边长.
(本小题满分13分)已知 ,命题
,命题 “函数
“函数 在
在 上单调递减”,
上单调递减”,
命题 “关于
“关于 的不等式
的不等式 对一切的
对一切的 恒成立”,若
恒成立”,若 为假命题,
为假命题, 为真命题,求实数
为真命题,求实数 的取值范围.
的取值范围.
. (本小题满分13分)已知数列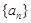 的前
的前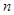 项和为
项和为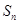 ,且
,且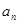 是
是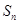 与2的等差中项,
与2的等差中项,
⑴求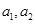 的值;
的值;
⑵求数列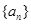 的通项公式。
的通项公式。
(13分,理科做)已知函数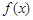 的定义域为
的定义域为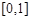 ,且同时满足:①
,且同时满足:①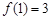 ;②
;②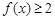 恒成立;③若
恒成立;③若 ,则有
,则有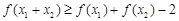 .
.
(1)试求函数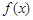 的最大值和最小值;
的最大值和最小值;
(2)试比较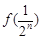 与
与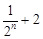 的大小
的大小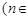 N);
N);
(3)某人发现:当x=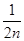 (nÎN)时,有f(x)<2x+2.由此他提出猜想:对一切xÎ(0,1
(nÎN)时,有f(x)<2x+2.由此他提出猜想:对一切xÎ(0,1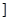 ,都有
,都有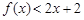 ,请你判断此猜想是否正确,并说明理由.
,请你判断此猜想是否正确,并说明理由.
(13分,文科做)设二次函数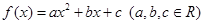 满足下列条件:
满足下列条件:
①当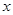 ∈R时,
∈R时,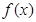 的最小值为0,且f (
的最小值为0,且f (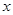 -1)=f(-
-1)=f(-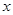 -1)成立;
-1)成立;
②当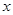 ∈(0,5)时,
∈(0,5)时,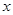 ≤
≤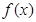 ≤2
≤2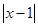 +1恒成立。
+1恒成立。
(1)求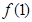 的值;
的值;
(2)求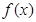 的解析式;
的解析式;
(3)求最大的实数m(m>1),使得存在实数t,只要当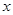 ∈
∈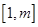 时,就有
时,就有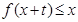 成立。
成立。