已知函数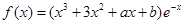
(1)如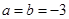 ,求
,求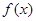 的单调区间;
的单调区间;
(2)若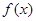 在
在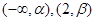 单调增加,在
单调增加,在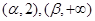 单调减少,
单调减少,
证明: o.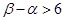
某班同学利用寒假在三个小区进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,这两族人数占各自小区总人数的比例如下:
(1)从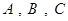 三个社区中各选一人,求恰好有2人是低碳族的概率;
三个社区中各选一人,求恰好有2人是低碳族的概率;
(2)在B小区中随机选择20户,从中抽取的3户中“非低碳族”数量为X,求X的分布列和期望EX.
如图,在四棱柱 中,侧面
中,侧面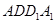 ⊥底面
⊥底面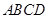 ,
, ,底面
,底面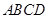 为直角梯形,其中
为直角梯形,其中
 ,O为
,O为 中点。
中点。
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求锐二面角A—C1D1—C的余弦值。
设数列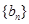 的前
的前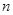 项和为
项和为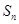 ,且
,且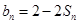 ;数列
;数列 为等差数列,且
为等差数列,且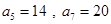 .
.
(1)求数列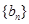 的通项公式;
的通项公式;
(2)若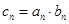 (
(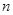 =1,2,3…),
=1,2,3…), 为数列
为数列 的前
的前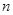 项和.求
项和.求 .
.
已知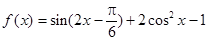
(Ⅰ)求函数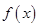 的单调增区间
的单调增区间
(Ⅱ)在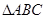 中,
中,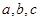 分别是角
分别是角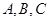 的对边,且
的对边,且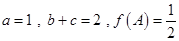 ,求
,求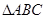 的面积
的面积
某糖果厂生产A、B两种糖果,A种糖果每箱可获利润40元,B种糖果每箱可获利润50元.其生产过程分混合、烹调、包装三道工序.下表为每箱糖果生产过程中所需平均时间(单位:min).
| 混合 |
烹调 |
包装 |
|
| A |
1 |
5 |
3 |
| B |
2 |
4 |
1 |
每种糖果的生产过程中,混合的设备至多用机器12 h,烹调的设备最多只能用机器30 h,包装的设备最多只能用机器15 h,每种糖果各生产多少箱可获得最大利润?