(本小题满分12分)已知函数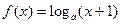 ,点
,点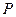 是函数
是函数 图像上任意一点,点
图像上任意一点,点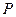 关于原点的对称点
关于原点的对称点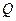 的轨迹是函数
的轨迹是函数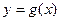 的图像. (Ⅰ)当
的图像. (Ⅰ)当 时,解关于
时,解关于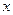 的不等式
的不等式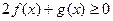 ; (Ⅱ)当
; (Ⅱ)当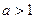 ,且
,且 时,总有
时,总有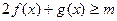 恒成立,求
恒成立,求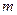 的取值范围.
的取值范围.
(本小题满 分12分)
分12分)
已知集合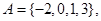 在平面直角坐标系中,点M的坐标
在平面直角坐标系中,点M的坐标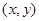 满足
满足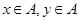 .
.
(1)请列出点M的所有坐标;
(2)求点M不在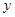 轴上的概率;
轴上的概率;
(3)求点M正好落在区域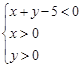 上的概率.
上的概率.
(本小题满分12分)
在△ABC中,角A、B、C的对边分别为a、b、c,且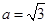 ,
,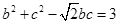 .
.
(1)求角A;
(2)设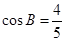 ,求边
,求边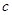 的大小.
的大小.
(本小题满分10分)
设函数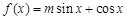
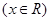 的图象经过点
的图象经过点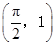 .
.
(1)求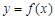 的解析式,并求函数的最小正周期.
的解析式,并求函数的最小正周期.
(2)若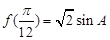 ,若
,若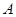 是面
是面 积为
积为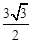 的锐角
的锐角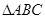 的内角,
的内角,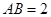 ,求
,求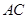 的长.
的长.
如图,点P是边长为1的菱形ABCD外一点,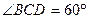 ,E是CD的中点,
,E是CD的中点,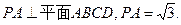
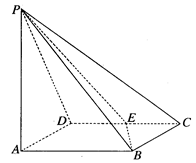
(1)证明:平面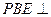 平面PAB;
平面PAB;
(2)求二面角A—BE—P的大小。
如图,正方形ABCD-A1B1C1D1中,E、F、G分别是AB,AD,AA1的中点,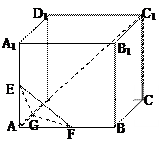
(1)求证AC1⊥平面EFG,
(2)求异面直线EF与CC1所成的角。