(12分)某银行准备新设一种定期存款业务,经预测,存款量与存款利率的平方成正比,比例系数为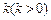 ,且知当利率为0.012时,存款量为1.44亿;又贷款的利率为
,且知当利率为0.012时,存款量为1.44亿;又贷款的利率为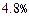 时,银行吸收的存款能全部放贷出去;若设存款的利率为
时,银行吸收的存款能全部放贷出去;若设存款的利率为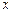 ,
,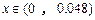 ;试写出存款量f(x)与存款利率的关系式,且当
;试写出存款量f(x)与存款利率的关系式,且当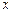 为多少时,银行可获得最大收益?
为多少时,银行可获得最大收益?
(本小题满分12分)为备战某次运动会,某市体育局组建了一个由4个男运动员和2个女运动员组成的6人代表队并进行备战训练.
(1)经过备战训练,从6人中随机选出2人进行成果检验,求选出的2人中至少有1个女运动员的概率;
(2)检验结束后,甲、乙两名运动员的成绩如下:
甲: ,
, ,
, ,
, ,
,
乙: ,
, ,
, ,
, ,
,
根据两组数据完成图示的茎叶图,并通过计算说明哪位运动员的成绩更稳定.
(本小题满分12分)已知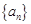 是公差不为零的等差数列,且
是公差不为零的等差数列,且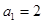 ,
, ,
,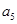 ,
,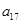 成等比数列.
成等比数列.
(1)求数列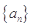 的通项公式;
的通项公式;
(2)设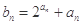 ,求数列
,求数列 的前
的前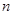 项和
项和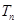 .
.
(本小题满分10分)选修4-5:不等式选讲
设函数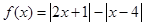 .
.
(1)解不等式: ;
;
(2)若 对一切实数
对一切实数 均成立,求
均成立,求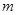 的取值范围.
的取值范围.
(本小题满分10分)选修4-4:坐标系与参数方程
在直角坐标系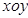 中,曲线
中,曲线 的参数方程为
的参数方程为 ,(
,(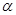 为参数),以原点
为参数),以原点 为极点,
为极点,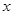 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线 的极坐标方程为
的极坐标方程为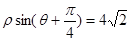 .
.
(1)求曲线 的普通方程与曲线
的普通方程与曲线 的直角坐标方程;
的直角坐标方程;
(2)设 为曲线
为曲线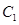 上的动点,求点
上的动点,求点 到
到 上点的距离的最小值.
上点的距离的最小值.
(本小题满分10分)选修4-1:几何证明选讲
如图, 是⊙
是⊙ 的直径,
的直径, 是弧
是弧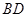 的中点,
的中点, ,垂足为
,垂足为 ,
,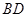 交
交 于点
于点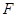 .
.
(1)求证: ;
;
(2)若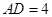 ,⊙
,⊙ 的半径为6,求
的半径为6,求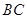 的长.
的长.