某蔬菜基地种植番茄，由历年市场行情得知，从二月一日起的300天内，番茄市场售价与上市时间的关系用图（1）的一条折线表示；番茄的种植成本与上市时间的关系用图（2）的抛物线表示.
（1）写出图1表示的市场售价与时间的函数关系式P＝f（t）；图2表示的种植成本与时间的函数关系式Q＝g（t）；
（2）市场售价减去种植成本为纯收益，问何时上市的番茄纯收益最大?（注：市场售价和种植成本的单位：元／102，ｋg，时间单位：天）
如图，公园有一块边长为2的等边△ABC的边角地，现修成草坪， 图中DE把草坪分成面积相等的两部分，D在AB上，E在AC上．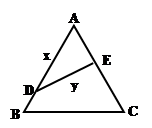
（1）设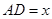
（x≥0），
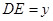，求用
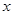表示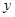
的函数关系式,并求函数的定义域；
（2）．如果
是灌溉水管，为节约成本，希望它最短，的位置应在哪里？如果是参观线路，则希望它最长，的位置又应在哪里？请予证明．
已知函数
（1）求函数的周期；
（2）求函数的单调递增区间；
（3）若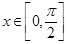
时，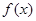
的最小值为– 2 ，求a的值．
在
分别是角A、B、C的对边，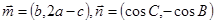
，且
．
（1）求角B的大小；
（2）求sin A＋sin C的取值范围．
已知向量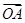
＝(3，－4)，
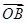＝(6，－3)，
＝(5－m，－3－m)．
（1）若点A，B，C不能构成三角形，求实数m满足的条件；
（2）若△ABC为直角三角形，求实数m的值．
(本小题满分12分)如图，椭圆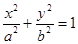
上的点M与椭圆右焦点
的连线
与x轴垂直，且OM（O是坐标原点）与椭圆长轴和短轴端点的连线AB平行．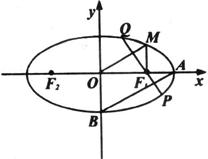
（1）求椭圆的离心率；
（2）过且与AB垂直的直线交椭圆于P、Q，若
的面积是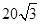
，求此时椭圆的方程．