已知双曲线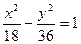 的顶点都是椭圆
的顶点都是椭圆 的顶点,直线
的顶点,直线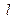 :
: 经过椭圆的一个焦点.⑴求椭圆的方程;⑵抛物线
经过椭圆的一个焦点.⑴求椭圆的方程;⑵抛物线 经过椭圆的两个焦点,与直线
经过椭圆的两个焦点,与直线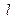 相交于
相交于 、
、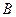 ,试将线段
,试将线段 的长
的长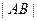 表示为
表示为 的函数.
的函数.
在△ABC中,内角A,B,C的对边分别为a,b,c.已知cosA= ,sinB=
,sinB= cosC.
cosC.
(1)求tanC的值;
(2)若a= ,求△ABC的面积.
,求△ABC的面积.
在△ABC中,内角A,B,C的对边分别为a,b,c.已知 =
= .
.
(1)求 的值;
的值;
(2)若B为钝角,b=10,求a的取值范围.
在△ABC中,a,b,c分别是三内角A,B,C所对的三边,已知b2+c2=a2+bc.
(1)求角A的大小;
(2)若2sin2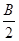 +2sin2
+2sin2 =1,试判断△ABC的形状.
=1,试判断△ABC的形状.
在△ABC中,a,b,c分别是角A,B,C的对边,向量m=(2sinB,2-cos2B),n=(2sin2(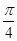 +
+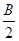 ),-1),且m⊥n.
),-1),且m⊥n.
(1)求角B的大小;
(2)求sinA+cosC的取值范围.
已知函数f(x)=cos2ωx+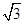 sinωxcosωx-
sinωxcosωx-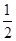 (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.
(1)求ω值及f(x)的单调递增区间;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,已知a=1,b=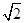 ,f(
,f(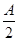 )=
)=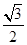 ,求角C的大小.
,求角C的大小.