(本小题满分14分)已知二次函数 .(1)若
.(1)若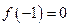 ,试判断函数
,试判断函数 零点个数;(2)若对
零点个数;(2)若对 且
且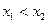 ,
, ,试证明
,试证明 ,使
,使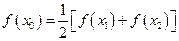 成立。(3)是否存在
成立。(3)是否存在 ,使
,使 同时满足以下条件①对
同时满足以下条件①对 ,且
,且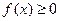 ;②对
;②对 ,都有
,都有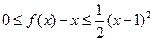 。若存在,求出
。若存在,求出 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
设等差数列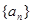 的公差
的公差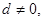 且
且 记
记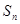 为数列
为数列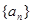 的前
的前 项和.
项和.
(1)若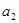 、
、 、
、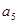 成等比数列,且
成等比数列,且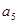 、
、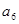 的等差中项为
的等差中项为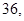 求数列
求数列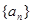 的通项公式;
的通项公式;
(2)若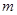 、
、 、
、 且
且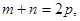 证明:
证明: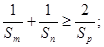
(3)若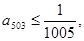 证明:
证明: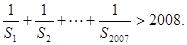
已知函数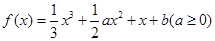 ,
, 为函数
为函数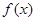 的导函数.
的导函数.
(1)设函数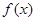 的图象与
的图象与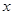 轴交点为
轴交点为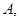 曲线
曲线 在
在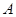 点处的切线方程是
点处的切线方程是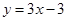 ,求
,求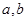 的值;
的值;
(2)若函数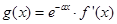 ,求函数
,求函数 的单调区间.
的单调区间.
某同学参加3门课程的考试.假设该同学第一门课程取得优秀成绩的概率为 第二、第三门课程取得优秀成绩的概率分别为
第二、第三门课程取得优秀成绩的概率分别为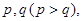 且不同课程是否取得优秀成绩相互独立,记
且不同课程是否取得优秀成绩相互独立,记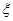 为该生取得优秀成绩的课程数,其分布列为
为该生取得优秀成绩的课程数,其分布列为
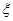 |
0 |
1 |
2 |
3 |
 |
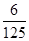 |
 |
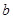 |
 |
(1)求该生至少有1门课程取得优秀成绩的概率;
(2)求 ,
,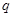 的值;
的值;
(3)求数学期望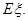
已知四棱锥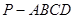 的底面
的底面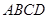 是边长为
是边长为 的正方形,
的正方形,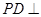 底面
底面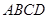 ,
,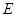 、
、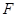 分别为棱
分别为棱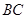 、
、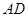 的中点.
的中点.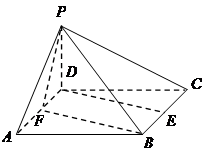
(1)求证: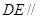 平面
平面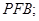
(2)已知二面角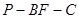 的余弦值为
的余弦值为 求四棱锥
求四棱锥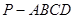 的体积.
的体积.
已知:以点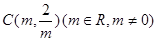 为圆心的圆与
为圆心的圆与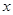 轴交于点
轴交于点 、
、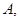 与
与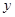 轴交于点
轴交于点 、
、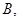 其中
其中 为原点.
为原点.
(1)求证: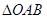 的面积为定值;
的面积为定值;
(2)设直线 与圆
与圆 交于点
交于点 、
、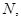 若
若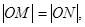 求⊙
求⊙ 的方程.
的方程.