材料的电阻率ρ随温度变化的规律为
，其中
称为电阻温度系数，
是材料在t="0" ℃时的电阻率，在一定的温度范围内是与温度无关的常量。金属的电阻一般随温度的增加而增加，有正温度系数；而某些非金属如碳等则相反，具有负温数系数。利用具有正负温度系数的两种材料的互补特性，可制成阻值在一定温度范围内不随温度变化的电阻。已知：在0 ℃时，铜的电阻率为
，碳的电阻率为
，在0 ℃附近，铜的电阻温度系数为3.9×10–3 ℃-1,碳的电阻温度系数为
。将横截面积相同的碳棒与铜棒串接成长1.0 m的导体，要求其电阻在0 ℃附近不随温度变化，求所需碳棒的长度(略碳棒和铜棒的尺寸随温度的变化).
一个物体以20 m/s的速度在空中飞行，突然由于内力作用物体分裂成质量为3∶7的两块.在这一瞬间，大物块以80 m/s的速度向原来方向飞去，则小物块飞行速度是多大？方向如何？
如图所示质量m="0.5" kg的木块以1 m/s的水平速度滑到在光滑水平面上静止的质量为M="2" kg的小车上，经过0.2 s木块和小车达到相同速度一起运动.求木块和小车间的动摩擦因数.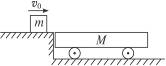
湖面上静止的一条小船（如图所示）长l="3" m，质量M="120" kg.质量为m="60" kg的人从船头走到船尾，求此过程中人和船相对于地面的位移s1、s2.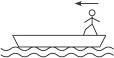
质量为2 kg的木块静止在光滑的水平面上，一颗质量为0.02 kg的子弹以500 m/s的速度从水平方向射入木块，射穿木块后子弹速度为100 m/s.求木块获得的速度大小.
在“验证动量守恒定律”的实验中，使用半径相同均为1 cm的两个小球A和B，它们的质量之比mA∶mB=3∶8，实验结果如图所示，O点为斜槽末端所装重垂线的竖直投影点，M、P、N为小球在白纸上的落点位置，且O、M、P、N在同一直线上.试用图示刻度尺上读出的数据和题设条件验证两小球碰撞前后的动量是否守恒.