(本小题满分12分)已知高二年级的某6名学生,独立回答某类问题时答对的概率都是0.5,而将这6名同学平均分为甲、乙、丙3个小组后,每个小组经过两名同学讨论后再回答同类问题时答对此类问题的概率都是0.7,若各个同学或各个小组回答问题时都是相互独立的.
(Ⅰ)这6名同学平均分成3组,共有分法多少种?
(Ⅱ)若分组后,3个小组中恰有2组能答对此类问题的概率是多少?
(Ⅲ)若要求独立回答,则这6名学生中至多有4人能答对此类问题的概率是多少?
设复数z=(m2+2m-3)+(m-1)i, 试求m取何值时
(1)Z是实数;
(2)Z是纯虚数;
(3)Z对应的点位于复平面的第一象限.
(本小题满分13分)在平面直角坐标系中,已知三个点的坐标分别为: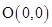 ,
,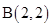 ,
,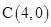 .
.
(1)若过点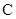 作一条直线
作一条直线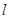 ,使点
,使点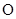 和点
和点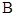 到直线
到直线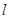 的距离相等,求直线
的距离相等,求直线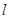 的方程;
的方程;
(2)求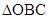 的外接圆的方程.
的外接圆的方程.
(本小题满分15分)如图,正方形 的边长为1,正方形
的边长为1,正方形 所在平面与平面
所在平面与平面 互相垂直,
互相垂直, 是
是 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证: ;
;
(3)求三棱锥 的体积.
的体积.
(1)利用“五点法”画出函数 在长度为一个周期的闭区间的简图
在长度为一个周期的闭区间的简图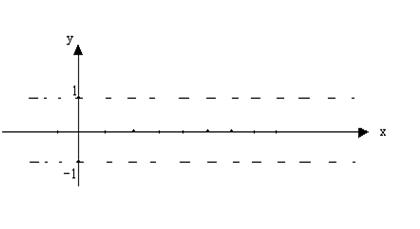
(2)并说明该函数图象可由y=sinx(x R)的图象经过怎样平移和伸缩变换得到的。
R)的图象经过怎样平移和伸缩变换得到的。
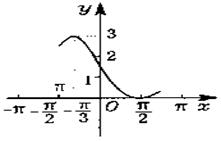
.已知函数y=Asin(ωx+φ)+b(A>0,|φ|<π,b为常数)的一段图象(如图)所示.
①求函数的解析式;②求这个函数的单调区间.