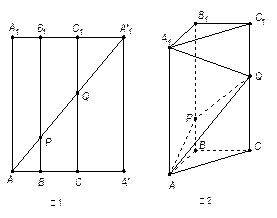 如图1所示,在边长为
如图1所示,在边长为 的正方形
的正方形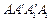 中,
中,
 ,且
,且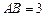 ,
,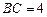 ,
, 分别交
分别交
 于点
于点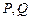 ,将该正方形沿
,将该正方形沿 、
、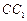 折叠,使得
折叠,使得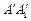 与
与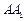 重合,构成如图2所示的三棱柱
重合,构成如图2所示的三棱柱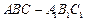 中
中
(Ⅰ)求证:
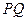 ;
;
(Ⅱ)在底边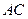 上有一点
上有一点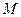 ,
,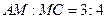 ,
,
求证: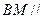 面
面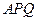
(III)求直线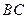 与平面
与平面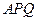 所成角的正弦值.
所成角的正弦值.
(本小题满分12分)已知公差大于零的等差数列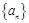 满足:
满足: .
.
(Ⅰ)求数列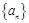 通项公式;
通项公式;
(Ⅱ)记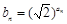 ,求数列
,求数列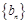 的前
的前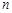 项和
项和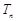 .
.
附加题: 对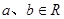 ,记
,记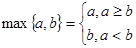 ,函数
,函数 .
.
(1)作出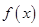 的图像,并写出
的图像,并写出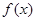 的解析式;
的解析式;
(2)若函数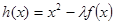 在
在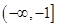 上是单调函数,求
上是单调函数,求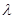 的的取值范围.
的的取值范围.
已知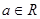 ,函数
,函数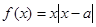 ,
,
(1)当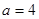 时,写出函数
时,写出函数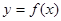 的单调递增区间;
的单调递增区间;
(2)当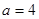 时,求
时,求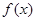 在区间
在区间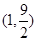 上最值;
上最值;
(3)设 ,函数
,函数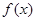 在
在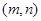 上既有最大值又有最小值,请分别求出
上既有最大值又有最小值,请分别求出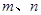 的取值范围(用
的取值范围(用 表示)
表示)
已知二次函数 的最小值为1,且
的最小值为1,且
(1)求 的解析式;
的解析式;
(2)若 在区间
在区间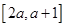 上是单调函数,求实数
上是单调函数,求实数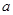 的取值范围.
的取值范围.
设函数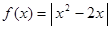
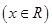 .
.
(1)先完成下列表格,再画出函数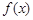 在区间
在区间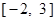 上的图像;
上的图像;
(2)根据图像写出该函数在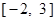 上的单调区间;
上的单调区间;
(3)根据图像写出该函数在区间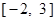 上的值域.
上的值域.
| x |
…… |
-2 |
0 |
1 |
2 |
3 |
…… |
| y |