已知:双曲线的顶点坐标(0,1),(0,-l),离心率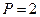 ,又抛物线
,又抛物线 的焦点与双曲线一个焦点重合.
的焦点与双曲线一个焦点重合.
(1)求抛物线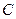 的方程;
的方程;
(2)已知 是
是 轴上的两点,过
轴上的两点,过 做直线与抛物线
做直线与抛物线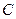 交于
交于 两点,试证:直线
两点,试证:直线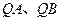 与
与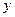 轴所成的锐角相等.
轴所成的锐角相等.
(3)在(2)的前提下,若直线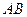 的斜率为1,问
的斜率为1,问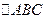 的面积是否有最大值?若有,求出最大值.若没有,说明理由.
的面积是否有最大值?若有,求出最大值.若没有,说明理由.
如图,四棱锥 S-ABCD的底面是正方形,每条侧棱的长都是地面边长的  倍,
倍,
P为侧棱SD上的点。 
(Ⅰ)求证: AC⊥ SD;
(Ⅱ)若 SD⊥ 平面 PAC,求二面角 P-AC-D的大小
(Ⅲ)在(Ⅱ)的条件下,侧棱SC上是否存在一点E,使得BE∥平
面PAC。若存在,求SE:EC的值  ;若不存在,试说明理由。
;若不存在,试说明理由。
求同时满足下列条件的所有的复数z,
①z+  ∈R, 且1<z+
∈R, 且1<z+  ≤6;②z的实部和虚部都是整数.
≤6;②z的实部和虚部都是整数.
已知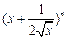 的展开式中前三项的系数成等差数列.
的展开式中前三项的系数成等差数列.
(Ⅰ)求n的值;(Ⅱ)求展开式中系数最大的项.
已知数列 满足 ,
(1)求 。
(2)由(1)猜想 的通项公式。
(3)用数学归纳法证明(2)的结果。
某校学生会有高一年级6人、高二年级5人、高三年级4人组成,
(1)选其中一人为校学生会主席,则不同的选有多少种;
(2)从3个年级中各选一个人出席一个会议,不同的选法有多少种;
(3)选不同年级的两人参加市里组织的活动,则不同的选法为多少种