(本小题满分14分)
已知数列 的前
的前 项和
项和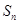 满足:
满足: ,
,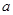 为常数,且
为常数,且 ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)若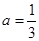 ,设
,设 ,且数列
,且数列 的前
的前 项和为
项和为 ,求证:
,求证: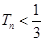 .
.
(本小题满分14分)
如图,四边形 是正方形,△
是正方形,△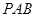 与△
与△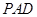 均是以
均是以 为直角顶点的等腰直角三角形,点
为直角顶点的等腰直角三角形,点 是
是 的中点,点
的中点,点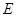 是边
是边 上的任意一点.
上的任意一点.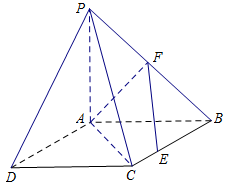
(1)求证: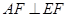 ;
;
(2)求二面角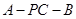 的平面角的正弦值.
的平面角的正弦值.
(本小题满分12分)
广州某商场根据以往某种商品的销售记录,绘制了日销售量的频率分布表(如表)和频率分布直方图(如图).
| 分组 |
频数 |
频率 |
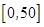 |
 |
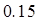 |
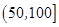 |
 |
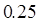 |
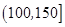 |
 |
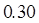 |
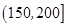 |
 |
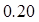 |
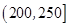 |
 |
 |

将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
(1)求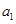 ,
,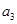 的值.
的值.
(2)求在未来连续3天里,有连续2天的日销售量都高于100个且另1天的日销售量不高于50
个的概率;
(3)用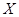 表示在未来3天里日销售量高于100个的天数,求随机变量
表示在未来3天里日销售量高于100个的天数,求随机变量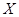 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)
已知函数
 R
R ,
,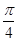 是函数
是函数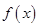 的一个零点.
的一个零点.
(1)求 的值,并求函数
的值,并求函数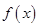 的单调递增区间;
的单调递增区间;
(2)若
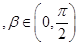 ,且
,且 ,
, ,求
,求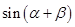 的值.
的值.
(本题14分)张老师居住在某城镇的A处,准备开车到学校B处上班。若该地各路段发生堵车事件都是独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图。(例如:A→C→D算作两个路段:路段AC发生堵车事件的概率为 ,路段CD发生堵车事件的概率为
,路段CD发生堵车事件的概率为 )。(1)请你为其选择一条由A到B的路线,使得途中发生堵车事件的概率最小;(2)若记路线A→C→F→B中遇到堵车次数为随机变量
)。(1)请你为其选择一条由A到B的路线,使得途中发生堵车事件的概率最小;(2)若记路线A→C→F→B中遇到堵车次数为随机变量 ,求
,求 的数学期望
的数学期望 。
。