设袋子中装有个红球，个黄球，个蓝球，且规定：取出一个红球得1分，取出一个黄球2分，取出蓝球得3分．
（1）当=3，=2，=1时，从该袋子中任取（有放回，且每球取到的机会均等）2个球，记随机变量为取出此2球所得分数之和．，求分布列；
（2）从该袋子中任取（且每球取到的机会均等）1个球，记随机变量为取出此球所得分数．若，求：：．
（本小题满分12分）已知函数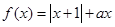
(
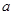∈R).
（1）画出当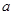=2时的函数
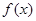的图象；
（2）若函数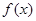在R上具有单调性，求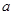的取值范围.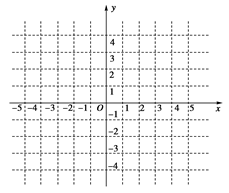
（本小题满分12分）某商品的进价为每件40元，售价为每件50元，每个月可卖出210件；如果每件商品在该售价的基础上每上涨1元，则每个月少卖10件（每件售价不能高于65元）．设每件商品的售价上涨
元（为正整数），每个月的销售利润为
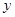元．(14分)
（1）求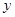与的函数关系式并直接写出自变量的取值范围；
（2）每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？
证明：函数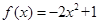
是偶函数，且在
上是减少的。（本小题满分12分）
（本小题满分12分）
已知
，求
的值
（本小题满分12分）
已知集合A＝{x| x2－3x－10≤0}，B＝{x| m＋1≤x≤2m－1}，若A
B且B≠
，求
实数m的取值范围。