已知函数
.
(1)求函数
的单调区间;
(2)证明:对任意的
,存在唯一的
,使
.
(3)设(2)中所确定的
关于
的函数为
,证明:当
时,有
.
已知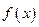 是定义在
是定义在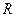 上的不恒为零的函数,且对于任意的
上的不恒为零的函数,且对于任意的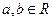 都满足:
都满足: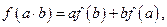 若
若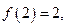 则
则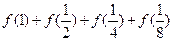 的值为( )
的值为( )
A.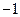 |
B.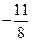 |
C.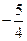 |
D.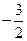 |
已知关于 的函数 ,其导函数为 。令 ,记函数 在区间[-1、1]上的最大值为 .
(Ⅰ)如果函数
在
处有极值-
,试确定
的值;
(Ⅱ)若
,证明对任意的
,都有
;
(Ⅲ)若
对任意的
恒成立,试求
的最大值。
围建一个面积为
的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为
的进出口,如图所示,已知旧墙的维修费用为45元
,新墙的造价为180元
,设利用的旧墙的长度为
(单位:元). 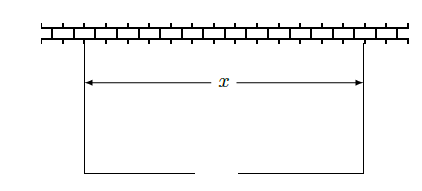
(Ⅰ)将
表示为
的函数;
(Ⅱ)试确定
,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
.要制造一种机器零件,甲机床废品率为 ,而乙机床废品率为
,而乙机床废品率为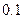 ,而它们的生产是独立的,从它们制造的产品中,分别任意抽取一件,求:
,而它们的生产是独立的,从它们制造的产品中,分别任意抽取一件,求:
(1)其中至少有一件废品的概率;(2)其中至多有一件废品的概率.
动点P从边长为1的正方形ABCD的顶点出发顺次经过B、C、D再回到A;设 表示P点的行程,
表示P点的行程, 表示PA的长,求
表示PA的长,求 关于
关于 的函数解析式.
的函数解析式.