下表给出一个“等差数阵”：
| 4 |
7 |
（ ） |
（ ） |
（ ） |
…… |
 |
…… |
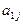| 7 |
12 |
（ ） |
（ ） |
（ ） |
…… |
 |
…… |
| （ ） |
（ ） |
（ ） |
（ ） |
（ ） |
…… |
 |
…… |
| （ ） |
（ ） |
（ ） |
（ ） |
（ ） |
…… |
 |
…… |
| …… |
…… |
…… |
…… |
…… |
…… |
…… |
…… |
 |
 |
 |
 |
 |
…… |
 |
…… |
| …… |
…… |
…… |
…… |
…… |
…… |
…… |
…… |
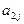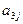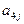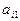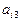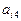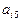其中每行、每列都是等差数列，表示位于第i行第j列的数。
（I）写出
的值；（II）写出的计算公式；
已知几何体A—BCED的三视图如图所示，其中俯视图和侧视图都是腰长为4的等腰直角三角形，正视图为直角梯形．
（1）求此几何体的体积V的大小;
（2）求异面直线DE与AB所成角的余弦值；
（3）试探究在DE上是否存在点Q，使得AQ
BQ并说明理由.
设函数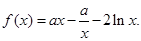
（Ⅰ）若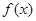
在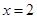
时有极值，求实数
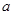的值和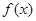的单调区间;
（Ⅱ）若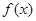在定义域上是增函数,求实数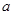的取值范围．
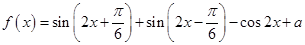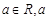已知函数
（
为常数）．
（1）求函数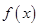
的最小正周期和单调增区间；
（2）若函数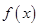的图像向左平移
个单位后，得到函数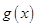
的图像关于
轴对称，求实数
的最小值.
甲乙丙三人商量周末去玩，甲提议去市中心逛街，乙提议去城郊觅秋，丙表示随意。最终，商定以抛硬币的方式决定结果。规则是：由丙抛掷硬币若干次，若正面朝上则甲得一分乙得零分，反面朝上则乙得一分甲得零分，先得4分者获胜，三人均执行胜者的提议.记所需抛币次数为
.
⑴求=6的概率；
⑵求的分布列和期望.
已知函数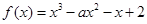
(
).
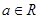（Ⅰ）当
时，求函数
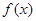的极值；
（Ⅱ）若对任意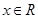
，不等式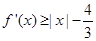
恒成立，求实数
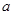的取值范围．