某厂家拟在2011年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)x万件与年促销费用m万元(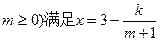 )(k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件。已知2008年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
)(k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件。已知2008年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将2011年该产品的利润y万元表示为年促销费用m万元的函数;
(2)该厂家2011年的促销费用投入多少万元时,厂家的利润最大?
已知数列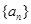 的通项
的通项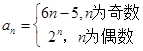 ,求数列
,求数列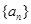 的前n项和
的前n项和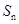 .
.
在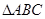 中,内角A,B,C所对的边分别为a,b,c,已知
中,内角A,B,C所对的边分别为a,b,c,已知 .
.
(1)求证:a,b,c成等比数列;
(2)若 ,求
,求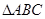 的面积S.
的面积S.
已知命题P:“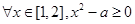 ”,q:“
”,q:“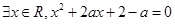 ”,若“
”,若“ ”是真命题,求实数a的取值范围.
”是真命题,求实数a的取值范围.
若圆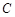 经过坐标原点和点
经过坐标原点和点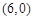 ,且与直线
,且与直线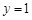 相切, 从圆
相切, 从圆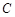 外一点
外一点 向该圆引切线
向该圆引切线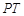 ,
, 为切点,
为切点,
(Ⅰ)求圆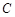 的方程;
的方程;
(Ⅱ)已知点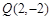 ,且
,且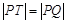 , 试判断点
, 试判断点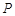 是否总在某一定直线
是否总在某一定直线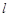 上,若是,求出
上,若是,求出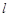 的方程;若不是,请说明理由;
的方程;若不是,请说明理由;
(Ⅲ)若(Ⅱ)中直线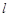 与
与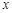 轴的交点为
轴的交点为 ,点
,点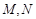 是直线
是直线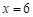 上两动点,且以
上两动点,且以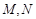 为直径的圆
为直径的圆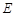 过点
过点 ,圆
,圆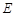 是否过定点?证明你的结论.
是否过定点?证明你的结论.
已知⊙M:x2+(y-2)2=1,Q是x轴上的动点,QA,QB分别切⊙M于A,B两点.
(Ⅰ)若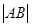 =
=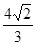 ,求
,求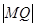 及直线MQ的方程;
及直线MQ的方程;
(Ⅱ)求证:直线AB恒过定点.