若圆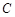 经过坐标原点和点
经过坐标原点和点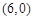 ,且与直线
,且与直线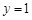 相切, 从圆
相切, 从圆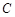 外一点
外一点 向该圆引切线
向该圆引切线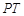 ,
, 为切点,
为切点,
(Ⅰ)求圆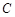 的方程;
的方程;
(Ⅱ)已知点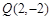 ,且
,且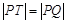 , 试判断点
, 试判断点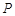 是否总在某一定直线
是否总在某一定直线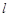 上,若是,求出
上,若是,求出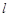 的方程;若不是,请说明理由;
的方程;若不是,请说明理由;
(Ⅲ)若(Ⅱ)中直线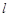 与
与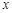 轴的交点为
轴的交点为 ,点
,点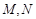 是直线
是直线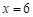 上两动点,且以
上两动点,且以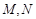 为直径的圆
为直径的圆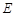 过点
过点 ,圆
,圆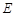 是否过定点?证明你的结论.
是否过定点?证明你的结论.
(本题满分12分)
已知函数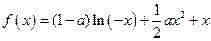
(I)如果 在
在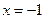 处的切线过(0,1)点,求
处的切线过(0,1)点,求 的值;
的值;
(II)若函数 在
在 为增函数,求实数
为增函数,求实数 的取值范围。
的取值范围。
(本题满分12分)
已知函数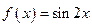 ,
,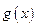 与
与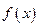 图象关于点
图象关于点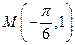 对称,
对称,
记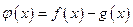
(Ⅰ) 求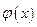 的最小正周期,单调增区间;
的最小正周期,单调增区间;
(Ⅱ) 若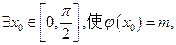 求
求 的最小值。
的最小值。
(本题满分12分)
在△ABC中,∠A、∠B、∠C所对的边长为a、b、c,已知
(Ⅰ)求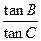 的值;
的值;
(Ⅱ)求∠A的取值范围。
(本小题满分14分)
椭圆 的离心率为
的离心率为 ,长轴端点与短轴端点间的距离为
,长轴端点与短轴端点间的距离为 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)过点 的直线
的直线 与椭圆
与椭圆 交于两点
交于两点 ,
, 为坐标原点,若
为坐标原点,若 ,求
,求
直线 的斜率
的斜率
(本小题满分13分)
某市4997名学生参加高中数学会考,得分均在60分
以上,现从中随机抽取一个容量为500的样本,制成
如图a所示的频率分布直方图.
(Ⅰ)由频率分布直方图可知本次会考的数学平均分为
81分.请估计该市得分在区间 的人数;
的人数;
(Ⅱ)如图b所示茎叶图是某班男女各4名学生的得分情况,
现用简单随机抽样的方法,从这8名学生中,抽取男
女生各一人,求女生得分不低于男生得分的概率.
 (第4题 图a) |