(本小题满分14分)
已知等比数列 的前
的前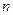 项和为
项和为
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设数列 满足
满足 ,
, 为数列
为数列 的前
的前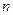 项和,试比较
项和,试比较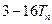 与
与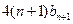 的大小,并证明你的结论.
的大小,并证明你的结论.
设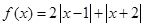 (1)求不等式
(1)求不等式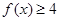 的解集;
的解集;
(2)若不等式 的解集是非空集合,求实数m的取值范围.
的解集是非空集合,求实数m的取值范围.
已知曲线 直线
直线
将直线 的极坐标方程和曲线的参数方程分别化为直角坐标方程和普通方程;
的极坐标方程和曲线的参数方程分别化为直角坐标方程和普通方程;
设点P在曲线C上,求点P到直线 的距离的最小值。
的距离的最小值。
如图,BA是圆O的直径,延长BA至E,使得AE=AO,过E点作圆O的割线交圆O于D、E,使AD=DC,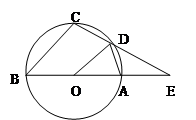
求证: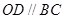 ;
;
若ED=2,求圆O的内接四边形ABCD的周长。
已知函数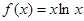 ,
,
(1)求函数 在
在 上的最小值;
上的最小值;
(2)若函数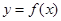 与
与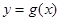 的图像恰有一个公共点,求实数a的值;
的图像恰有一个公共点,求实数a的值;
(3)若函数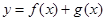 有两个不同的极值点
有两个不同的极值点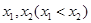 ,且
,且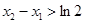 ,求实数a的取值范围。
,求实数a的取值范围。
已知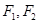 是椭圆的左、右焦点,O为坐标原点,点P
是椭圆的左、右焦点,O为坐标原点,点P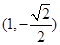 在椭圆上,线段
在椭圆上,线段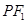 与y轴的交点M满足
与y轴的交点M满足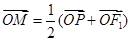
(Ⅰ) 求椭圆的标准方程;
(Ⅱ) 圆O是以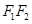 为直径的圆,直线
为直径的圆,直线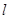 :
: 与圆相切,并与椭圆交于不同的两点
与圆相切,并与椭圆交于不同的两点 ,当
,当 ,且满足
,且满足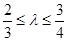 时,求直线
时,求直线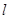 的方程。
的方程。