一个小正方体的六个面,三个面上标以数字0,两个面上标以数学1,一个面上标以数字2
(1)甲、乙两人各抛掷一次,谁的点数大谁就胜,求甲获胜的概率
(2)将这个小正方体抛掷两次,用随机变量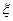 表示向上点数之积,求随机变量
表示向上点数之积,求随机变量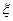 的概率分布列及数学期望
的概率分布列及数学期望
(本题满分14分)已知函数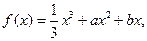 且
且

(1)试用含 的代数式表示
的代数式表示 ;
;
(2)求 的单调区间.
的单调区间.
(本题满分14分) 在平面直角坐标系 中,已知圆心在直线
中,已知圆心在直线 上,半径为
上,半径为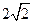 的圆C经过坐标原点O.
的圆C经过坐标原点O.
(1)求圆C的方程;
(2)是否存在直线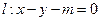 与圆C交于不同的两点A、B,且线段AB的中点恰在抛物线
与圆C交于不同的两点A、B,且线段AB的中点恰在抛物线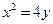 上,若
上,若 存在请求出m的值,若
存在请求出m的值,若 不存在请说明理由.
不存在请说明理由.
(本题满分14分)
如图,圆锥的顶点是S,底面中心为O.OC是与底面直径AB垂直的一条半径,D是母线SC的中点.
(1)求证:BC与SA不可能垂直.
(2)设圆锥的高为4,异面直线AD与BC所成角的余弦值为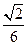 ,求圆锥的体积.
,求圆锥的体积.
(本题满分12分)已知A(2,0),B(0,2),C(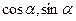 ),且0<
),且0< <
<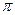 .
.
(1)若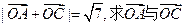 的夹角;
的夹角;
(2)若 的值.
的值.
已知函数 满足
满足 ,
, 是不为
是不为 的实常数。
的实常数。
(1)若当 时,
时, ,求函数
,求函数 的值域;
的值域;
(2)在(1)的条件下,求函数 的解析式;
的解析式;
(3)若当 时,
时, ,试研究函数
,试研究函数 在区间
在区间 上是否可能是单调函数?
上是否可能是单调函数?
若可能,求出 的取值范围;若不可能,请说明理由。
的取值范围;若不可能,请说明理由。