已知:三次函数 ,在
,在 上单调增,在(-1,2)上单调减,当且仅当
上单调增,在(-1,2)上单调减,当且仅当 时,
时,
|
(1)求函数f (x)的解析式; (2)若函数 ,求
,求 的单调区间.
的单调区间.
已知函数
(1)当 时,求函数
时,求函数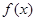 的极值;
的极值;
(2)当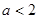 时,讨论函数
时,讨论函数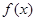 零点的个数.
零点的个数.
已知命题p:| |≤ 2;命题
|≤ 2;命题 .若
.若 是
是 的必要而不充分条件,求实数
的必要而不充分条件,求实数 的取值范围.
的取值范围.
已知函数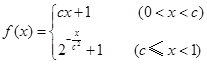 满足
满足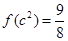 .
.
(1)求常数 的值;
的值;
(2)求使 成立的
成立的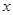 的取值范围.
的取值范围.
下图是利用计算机作图软件在直角坐标平面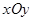 上绘制的一列抛物线和一列直线,在焦点为
上绘制的一列抛物线和一列直线,在焦点为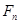 的抛物线列
的抛物线列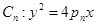 中,
中,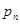 是首项和公比都为
是首项和公比都为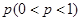 的等比数列,过
的等比数列,过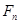 作斜率2的直线
作斜率2的直线 与
与 相交于
相交于 和
和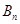 (
( 在
在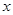 轴的上方,
轴的上方,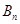 在
在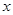 轴的下方).
轴的下方).
证明: 的斜率是定值;
的斜率是定值;
求 、
、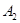 、
、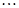 、
、 、
、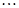 所在直线的方程;
所在直线的方程;
记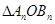 的面积为
的面积为 ,证明:数列
,证明:数列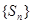 是等比数列,并求所有这些三角形的面积的和.
是等比数列,并求所有这些三角形的面积的和.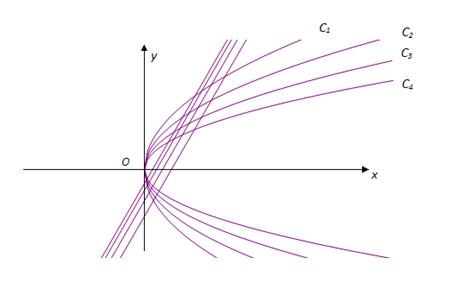
如图,四棱柱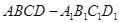 中, 侧棱
中, 侧棱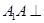 底面
底面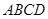 ,
,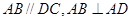 ,
,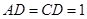 ,
, ,
,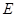 为棱
为棱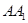 的中点.
的中点. 
(1)证明: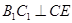 ;
;
(2)求异面直线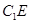 与
与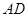 所成角的大小.(结果用反三角函数值表示)
所成角的大小.(结果用反三角函数值表示)