平面直角坐标系中,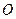 为坐标原点,给定两点
为坐标原点,给定两点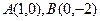 ,点
,点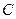 满足
满足 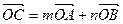 ,其中
,其中 ,且
,且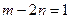 . (1)求点
. (1)求点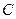 的轨迹方程;(2)设点
的轨迹方程;(2)设点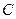 的轨迹与双曲线
的轨迹与双曲线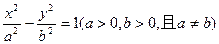 交于
交于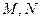 两点,且以
两点,且以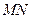 为直径的圆过原点,求证:
为直径的圆过原点,求证: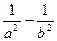 为定值;(3)在(2)的条件下,若双曲线的离心率不大于
为定值;(3)在(2)的条件下,若双曲线的离心率不大于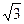 ,求双曲线实轴长的取值范围.
,求双曲线实轴长的取值范围.
(本小题满分12分)
如图,四棱柱 中,
中, 平面
平面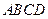 ,底面
,底面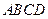 是边长为
是边长为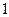 的正方形,侧棱
的正方形,侧棱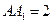 .
.
(1)求证: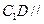 平面
平面 ;
;
(2)求直线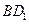 与平面
与平面 所成角的正弦值.
所成角的正弦值.
.(本小题满分12分)
在“自选模块”考试中,某考场的每位同学都选作了一道数学题,第一小组选《不等式选讲》的有1人,选《坐标系与参数方程 》的有5人;第二小组选《不等式选讲》的有2人,选《坐标系与参数方程》的有4人. 现从第一、第二两小组各任选2人分析得分情况.
》的有5人;第二小组选《不等式选讲》的有2人,选《坐标系与参数方程》的有4人. 现从第一、第二两小组各任选2人分析得分情况.
(1)求选出的4 人均为选《坐标系与参数方程》的概率;
(2)设 为选出的4个人中选《不等式选讲》的人数,求
为选出的4个人中选《不等式选讲》的人数,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分10分)
已知向量 设
设 (
( ,且
,且 为常数).
为常数).
(1)求 的最小正周期;
的最小正周期;
(2)若 在
在 上的最大值与最小值之和为7,求
上的最大值与最小值之和为7,求 的值.
的值.
已知函数
(1)若P=3,求曲线 在点(1,
在点(1, )处的切线方程;
)处的切线方程;
(2)若P>0且函数 在其定义域内为增函数,求实数P的取值范围;
在其定义域内为增函数,求实数P的取值范围;
(3)若函数 存在极值,求实数P的取值范围。
存在极值,求实数P的取值范围。
某企业2010年的纯利润为500万元,因设备老化等原因,企业的生产能力将逐年下降。若不能进行技术改造,预测从今年起每年比上一年纯利润减少20万元,今年初该企业一次性投入资金600万元进行技术改造,预测在 末扣除技术资金的情况下,第n年(2011年为第一年)的利润为500(1+
末扣除技术资金的情况下,第n年(2011年为第一年)的利润为500(1+ )万元(n为正整数)
)万元(n为正整数)
(1)设从今年起的前n年,若该企业不进行技术改造的累计纯利润为 万元,进行技术改造后的累计纯利润为
万元,进行技术改造后的累计纯利润为 万元(须扣除技术改造资金),求
万元(须扣除技术改造资金),求 、
、 的表达式;
的表达式;
(2)依上述预测,从今年起该企业至少经过多少年,进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润?