(本小题满分12分)
设函数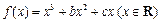 ,已知
,已知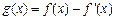 是奇函数.
是奇函数.
(1) 求b、c的值;
求b、c的值;
(2) 求
求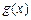 的单调区间与极值.
的单调区间与极值.
已知Sn=1+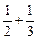 +…+
+…+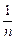 ,(n∈N*),设f(n)=S2n+1-Sn+1,试确定实数m的取值范围,使得对于一切大于1的自然数n,不等式:
,(n∈N*),设f(n)=S2n+1-Sn+1,试确定实数m的取值范围,使得对于一切大于1的自然数n,不等式:
f(n)>[logm(m-1)]2-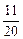 [log(m-1)m]2恒成立.
[log(m-1)m]2恒成立.
设{an}是正数组成的数列,其前n项和为Sn,并且对于所有的自然数n,an与2的等差中项等于Sn与2的等比中项.
(1)写出数列{an}的前3项.
(2)求数列{an}的通项公式(写出推证过程).
(3)令bn= (n∈N*),求
(n∈N*),求 (b1+b2+b3+…+bn-n).
(b1+b2+b3+…+bn-n).
设An为数列{an}的前n项和,An= (an-1),数列{bn}的通项公式为bn=4n+3;
(an-1),数列{bn}的通项公式为bn=4n+3;
(1)求数列{an}的通项公式;
(2)把数列{an}与{bn}的公共项按从小到大的顺序排成一个新的数列,证明:数列{dn}的通项公式为dn=32n+1;
(3)设数列{dn}的第n项是数列{bn}中的第r项,Br为数列{bn}的前r项的和;Dn为数列{dn}的前n项和,Tn=Br-Dn,求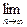

已知数列{an}是公差为d的等差数列,数列{bn}是公比为q的(q∈R且q≠1)的等比数列,若函数f(x)=(x-1)2,且a1=f(d-1),a3=f(d+1),b1=f(q+1),b3=f(q-1),
(1)求数列{an}和{bn}的通项公式;
(2)设数列{cn}的前n项和为Sn,对一切n∈N*,都有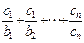 =an+1成立,求
=an+1成立,求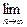


设等比数列{an}的各项均为正数,项数是偶数,它的所有项的和等于偶数项和的4倍,且第二项与第四项的积是第3项与第4项和的9倍,问数列{lgan}的前多少项和最大?(lg2=0.3,lg3=0.4)