设{an}是正数组成的数列,其前n项和为Sn,并且对于所有的自然数n,an与2的等差中项等于Sn与2的等比中项.
(1)写出数列{an}的前3项.
(2)求数列{an}的通项公式(写出推证过程).
(3)令bn= (n∈N*),求
(n∈N*),求 (b1+b2+b3+…+bn-n).
(b1+b2+b3+…+bn-n).
设数列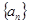 的前
的前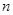 项和为
项和为 ,对任意的正整数
,对任意的正整数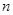 ,都有
,都有 成立,记
成立,记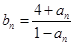 .(1)(1)求数列
.(1)(1)求数列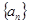 与数列
与数列 的通项公式;
的通项公式;
(2)设数列 的前
的前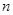 项和为
项和为 ,是否存在正整数
,是否存在正整数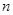 ,使得
,使得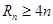 成立?若存在,找出一个正整数
成立?若存在,找出一个正整数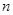 ;若不存在,请说明理由.
;若不存在,请说明理由.
(3)记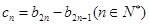 ,设数列
,设数列 的前
的前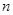 项和为
项和为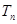 ,求证:对于
,求证:对于 都有
都有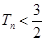
已知等比数列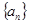 中各项均为正,有
中各项均为正,有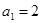 ,
,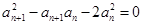 ,
,
等差数列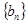 中,
中,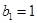 ,点
,点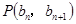 在直线
在直线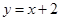 上.
上.
(1)求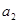 和
和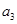 的值;(2)求数列
的值;(2)求数列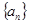 ,
,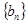 的通项
的通项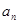 和
和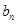 ;
;
(3)设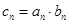 ,求数列
,求数列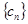 的前n项和
的前n项和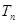 .
.
如图,要计算西湖岸边两景点B与C的距离,由于地形的限制,需要在岸上选取A和D两点,现测得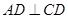 ,
,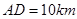 ,
,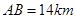 ,
,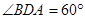 ,
,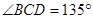 ,求两景点B与C的距离.
,求两景点B与C的距离.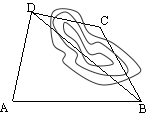
已知向量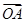 =(3,-4),
=(3,-4),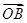 =(6,-3),
=(6,-3),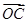 =(5-m,-3-m).
=(5-m,-3-m).
(1)若点A,B,C不能构成三角形,求实数m满足的条件;
若△ABC为直角三角形,求实数m的值.
在△ABC中,A、B、C是三角形的三内角,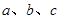 是三内角对应的三边,已知
是三内角对应的三边,已知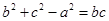 .(1)求角A的大小;(2)若
.(1)求角A的大小;(2)若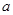 =
=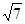 ,且△ABC的面积为
,且△ABC的面积为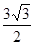 ,求
,求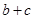 的值.
的值.