已知数列{an}是公差为d的等差数列，数列{bn}是公比为q的(q∈R且q≠1)的等比数列，若函数f(x)=(x－1)2，且a1=f(d－1)，a3=f(d+1)，b1=f(q+1)，b3=f(q－1)，
(1)求数列{an}和{bn}的通项公式；
(2)设数列{cn}的前n项和为Sn，对一切n∈N*，都有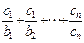
=an+1成立，求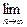
判断下列函数的奇偶性.
（1）f(x)=
;
(2)f(x)=log2(x+
) (x∈R);
(3)f(x)=lg|x-2|.
已知函数y=f(x)对任意x,y∈R均有f(x)+f(y)=f(x+y),且当x＞0时，f(x)＜0,f(1)="-" 
.
(1)判断并证明f(x)在R上的单调性；
（2）求f(x)在［-3，3］上的最值.
已知f(x)=
(x≠a).
（1）若a=-2,试证f(x)在（-∞,-2）内单调递增；
（2）若a＞0且f(x)在（1,+∞）内单调递减，求a的取值范围.
函数f(x)对任意的实数m、n有f(m+n)=f(m)+f(n),且当x＞0时有f(x)＞0.
（1）求证：f(x)在（-∞,+∞)上为增函数；
（2）若f(1)=1,解不等式f［log2(x2-x-2)］＜2.
已知f(x)在定义域（0，+∞）上为增函数，且满足f(xy)=f(x)+f(y),f(3)=1,试解不等式f(x)+f(x-8)≤2.