(本小题满分14分)数列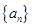 (
( )的前
)的前 项和
项和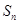 满足
满足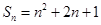 .
.
(1)求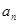 ;
;
(2)若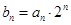 ,设数列
,设数列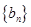 的前
的前 项和为
项和为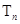 ,求
,求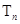 .
.
(本小题满分14分)如图,直三棱柱 中,
中,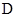 ,
,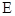 分别是
分别是 ,
,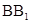 的中点.
的中点.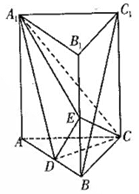
(1)证明: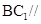 平面
平面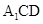 ;
;
(2)设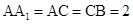 ,
,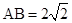 ,求三棱锥
,求三棱锥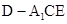 的体积.
的体积.
(本小题满分12分)以下茎叶图记录了甲、乙两组各三名同学在期末考试中的数学成绩.乙组
记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以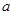 表示.
表示. 
(1)若甲、乙两个小组的数学平均成绩相同,求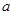 的值;
的值;
(2)求乙组平均成绩超过甲组平均成绩的概率.
【原创】(本小题满分12分)已知函数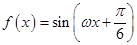 (
( )的最小正周期是
)的最小正周期是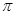 .
.
(1)求 的值;
的值;
(2)若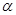 ,
, ,
, ,
,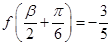 ,求
,求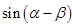 的值.
的值.
(本小题满分14分)已知函数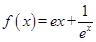 .
.
(1)求函数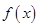 的最小值;
的最小值;
(2)若对所有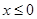 都有
都有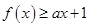 ,求实数
,求实数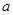 的取值范围.
的取值范围.