(本小题满分12分) 已知正三棱柱ABC-A1B1C1的各条棱长都为a,P为A1B上的点,且PC⊥AB. (Ⅰ)求二面角P-AC-B的正切值; (Ⅱ)求点B到平面PAC的距离.
已知函数 的部分图象如图所示,
的部分图象如图所示, 是图象的最高点,
是图象的最高点,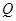 为图象与
为图象与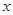 轴的交点,
轴的交点, 为坐标原点,若
为坐标原点,若
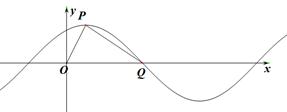
(1)求函数 的解析式,
的解析式,
(2)将函数 的图象向右平移2个单位后得到函数
的图象向右平移2个单位后得到函数 的图象,当
的图象,当 时,求函数
时,求函数 的值域.
的值域.
选修4—5:不等式选讲
已知函数 .
.
(Ⅰ)当 时,解不等式
时,解不等式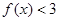 ;
;
(Ⅱ)若 的最小值为1,求a的值.
的最小值为1,求a的值.
选修4—4:坐标系与参数方程
已知曲线 的参数方程为
的参数方程为 (
(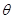 为参数),在同一平面直角坐标系中,将曲线
为参数),在同一平面直角坐标系中,将曲线 上的点按坐标变换
上的点按坐标变换 得到曲线
得到曲线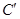 .(1)求曲线
.(1)求曲线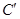 的普通方程; (2)若点
的普通方程; (2)若点 在曲线
在曲线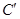 上,点
上,点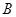
 ,当点
,当点 在曲线
在曲线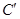 上运动时,求
上运动时,求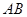 中点
中点 的轨迹方程.
的轨迹方程.
选修4-1:几何证明选讲
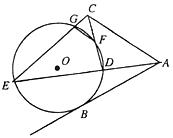
如图, 是
是 的一条切线,切点为
的一条切线,切点为 ,直线
,直线 ,
, ,
, 都是
都是 的割线,已知
的割线,已知 .
.
(1)求证: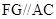 ;
;
(2)若 ,
, .求
.求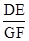 的值.
的值.
已知函数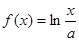 .
.
(1)若曲线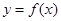 在
在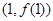 处的切线为
处的切线为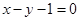 ,求
,求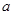 的值;
的值;
(2)设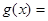
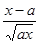 ,
,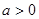 ,证明:当
,证明:当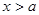 时,
时,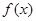 的图象始终在
的图象始终在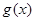 的图象的下方;
的图象的下方;
(3)当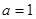 时,设
时,设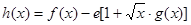 ,(
,(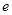 为自然对数的底数),
为自然对数的底数),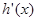 表示
表示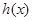 导函数,求证:对于曲线
导函数,求证:对于曲线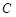 上的不同两点
上的不同两点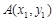 ,
,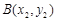 ,
,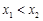 ,存在唯一的
,存在唯一的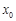
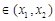 ,使直线
,使直线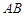 的斜率等于
的斜率等于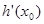 .
.