某车队2008年初以98万元购进一辆大客车,并投入营运,第一年需支出各种费用12万元,从第二年起每年支出费用均比上一年增加4万元,该车投入营运后每年的票款收入为50万元,设营运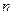 年该车的盈利总额为
年该车的盈利总额为 万元.
万元.
(1)写出 关于
关于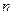 的函数关系式; (2)从哪一年开始,该汽车开始获利; (3)有两种方案处理该车:方案1——当盈利总额达最大值时,年底以20万元的价格卖掉该车;
的函数关系式; (2)从哪一年开始,该汽车开始获利; (3)有两种方案处理该车:方案1——当盈利总额达最大值时,年底以20万元的价格卖掉该车;
方案2——当年均盈利额最大时,年底以40万元的价格卖掉该车.试问车队以哪种方案处理该车获利较大?
在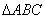 中,角A,B,C的对边分别为
中,角A,B,C的对边分别为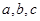 ,且满足
,且满足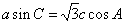 ,
, .
.
(Ⅰ)求角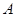 ;(Ⅱ)求
;(Ⅱ)求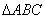 的面积;(Ⅲ)若
的面积;(Ⅲ)若 ,求边
,求边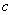 与
与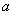 的值.
的值.
已知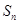 为各项均为正数的等比数列
为各项均为正数的等比数列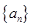 的前n项和,且
的前n项和,且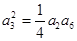 ,
, 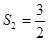
(I)求数列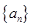 的通项公式;(II)若
的通项公式;(II)若 ,求n的最小值。
,求n的最小值。
已知函数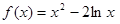 .
.
(Ⅰ)求函数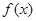 的单调区间;
的单调区间;
(Ⅱ)若存在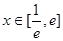 ,使不等式
,使不等式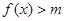 成立,求实数
成立,求实数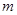 的取值范围;
的取值范围;
(Ⅲ)若关于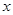 的方程
的方程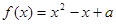 在区间
在区间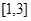 上恰好有两个不相等的实根,求实数
上恰好有两个不相等的实根,求实数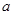 的取值范围.
的取值范围.
已知定义域为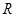 的函数
的函数 是奇函数.
是奇函数.
(Ⅰ)求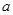 的值;
的值;
(Ⅱ)判断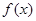 的单调性,并证明你的结论;
的单调性,并证明你的结论;
(Ⅲ)若对任意的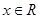 ,不等式
,不等式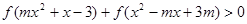 恒成立,求
恒成立,求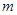 的取值范围.
的取值范围.
某商场销售某件商品的经验表明,该商品每日的销量 (单位:千克)与销售价格
(单位:千克)与销售价格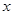 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式 ,其中
,其中 ,
,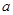 为常数。已知销售价格为5元/千克时,每日可售出该商品11千克。
为常数。已知销售价格为5元/千克时,每日可售出该商品11千克。
(Ⅰ)求实数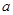 的值;
的值;
(Ⅱ)若该商品的成本为3元/千克,试确定销售价格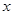 的值,使商场每日销售该商品所获得的利润最大。
的值,使商场每日销售该商品所获得的利润最大。