已知函数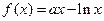
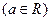 ,
,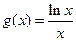 ,其中
,其中 (1)若
(1)若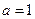 ,求
,求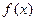 的极小值;(2)在(1)条件下证明
的极小值;(2)在(1)条件下证明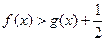 ;(3)是否存在实数
;(3)是否存在实数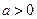 ,使
,使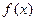 的最小值为3,如果存在,求出实数
的最小值为3,如果存在,求出实数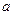 的值,若不存在,说明理由.
的值,若不存在,说明理由.
已知向量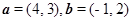 .
.
(1)求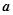 与
与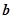 的夹角的余弦值;
的夹角的余弦值;
(2)若向量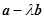 与
与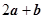 平行,求
平行,求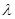 的值.
的值.
(本小题满分14分)已知点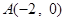 ,
,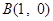 ,动点
,动点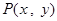 满足
满足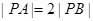 ,
, .
.
(1)求点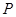 的轨迹方程;
的轨迹方程;
(2)求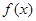 的解析式;
的解析式;
(3)判断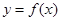 的图像与点
的图像与点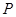 的轨迹的位置关系.
的轨迹的位置关系.
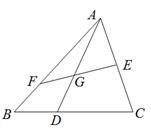
(本小题满分13分)如图,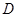 、
、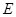 、
、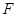 分别是
分别是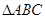 的边
的边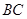 、
、 、
、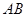 上的点,
上的点,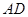 与
与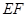 相交于
相交于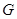 ,已知
,已知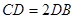 ,
,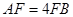 ,
,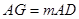 ,
,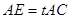 .
.
(1)试用 、
、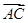 表示
表示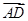 ;
;
(2)若 ,求
,求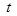 的值.
的值.
(本小题满分14分)为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打篮球时间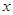 (单位:小时)与当天投篮命中率
(单位:小时)与当天投篮命中率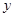 之间的关系:
之间的关系:
时间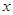 |
1 |
2 |
3 |
4 |
5 |
命中率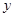 |
0.4 |
0.5 |
0.6 |
0.6 |
0.4 |
(1)根据上表提供的数据,求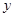 关于
关于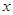 的线性回归方程
的线性回归方程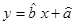
(2)预测小李该月6号打6小时篮球的投篮命中率是多少?
(参考公式:用最小二乘法求线性回归方程系数公式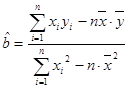 ,
,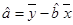 .)
.)
(本小题满分12分)在正三棱锥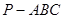 中,
中,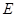 、
、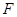 分别为棱
分别为棱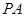 、
、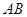 的中点,且
的中点,且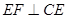 .
.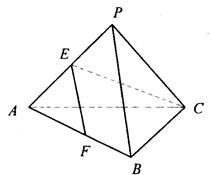
(1)求证:直线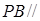 平面
平面 ;
;
(2)求证:平面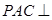 平面
平面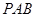 .
.