一批产品共100件,其中有10件是次品,为了检验其质量,从中以随机的方式选取5件,求在抽取的这5件产品中次品数分布列与期望值,并说明5件中有3件以上(包括3件)为次品的概率.(精确到0.001)
分析:根据题意确定随机变量及其取值,对于次品在3件以上的概率是3,4,5三种情况的和.
提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度 (单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车速度为0;当车流密度不超过20辆/千米时,车流速度为60千米,/小时,研究表明:当
(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车速度为0;当车流密度不超过20辆/千米时,车流速度为60千米,/小时,研究表明:当 时,车流速度v是车流密度
时,车流速度v是车流密度 的一次函数.
的一次函数.
(Ⅰ)当 时,求函数
时,求函数 的表达式;
的表达式;
(Ⅱ)当车流密度 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)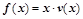 可以达到最大,并求出最大值.(精确到1辆/小时)
可以达到最大,并求出最大值.(精确到1辆/小时)
(本小题满分14分)
如图①边长为1的正方形ABCD中,点E、F分别
为AB、BC的中点,将△BEF剪去,将
△AED、△DCF分别沿DE、DF折起,使A、
C两点重合于点P得一个三棱锥如图②示.
(1)求证: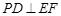 ;
;
(2)求三棱锥 的体积;
的体积;
(3)求DE与平面PDF所成角的正弦值.

(本小题满分12分) 随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图4.( )
)
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
(本小题满分12分)已知函数 (其中
(其中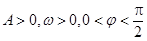 )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为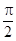 ,且图象上一个最低点为
,且图象上一个最低点为 .
.
(1)求 的解析式;
的解析式;
(2)当 ,求
,求 的值域.
的值域.
.如图,四边形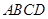 为矩形,
为矩形,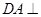 平面
平面 ,
, ,
, 平面
平面 于点
于点 ,且点
,且点 在
在 上.
上.
(1)求证: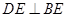 ;(2)求四棱锥
;(2)求四棱锥 的体积;
的体积;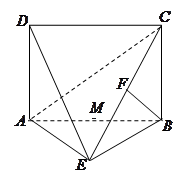
(3)设点 在线段
在线段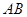 上,且
上,且 ,试在线段
,试在线段 上确定一点
上确定一点 ,使得
,使得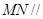 平面
平面 .
.