(本小题满分10分)如图,已知面积为1的正三角形ABC三边的中点分别为D、E、F,从A,B,C,D,E,F六个点中任取三个不同的点,所构成的三角形的面积为X(三点共线时,规定X=0)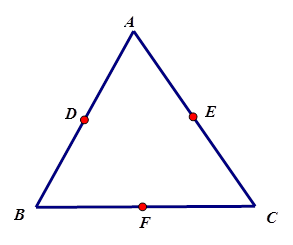
(1)求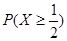 ;
;
(2)求E(X)
(每小题5分,满分15分)
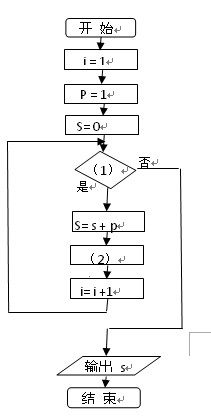
(1)已知如下程序框图,则输出的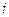 值是____________
值是____________
(2)该程序框图的功能是_________________________________

(3).按下列程序框图运算:规定:程序运行到“判断结果是否大于244”为1次运算,若x=5,则运算进行___________次才停止。
(4)给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推. 要求计算这50个数的和.将下面给出的程序框图补充完整 (1)________________________
(2)________________________ 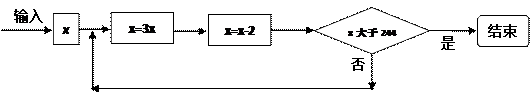
(每小题5分,满分10分)
(1)计算: 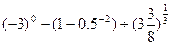
(2)已知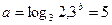 用
用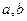 表示
表示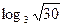 .
.
已知函数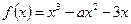
(1)若 在区间[1,+∞)上是增函数,求实数a的取值范围;
在区间[1,+∞)上是增函数,求实数a的取值范围;
(2)若x=-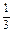 是
是 的极值点,求
的极值点,求 在[1,a]上的最大值;
在[1,a]上的最大值;
(3)在(2)的条件下,是否存在实数b,使得函数 =bx的图象与函数
=bx的图象与函数 的图象恰有3个交点,若存在,请求出实数b的取值范围;若不存在,试说明理由.
的图象恰有3个交点,若存在,请求出实数b的取值范围;若不存在,试说明理由.
(本小题满分12分)已知定义域为R的函数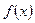 为奇函数,且满足
为奇函数,且满足 ,当x∈[0,1]时,
,当x∈[0,1]时,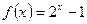 .
.
(1)求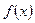 在[-1,0)上的解析式;
在[-1,0)上的解析式;
(2)求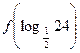 .
.
(本小题满分12分)数列{an}的前n项和记为Sn,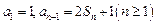
(1)求{an}的通项公式;
(2)等差数列{bn}的各项为正,其前n项和为Tn,且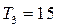 ,又
,又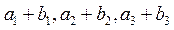 成等比数列,求Tn
成等比数列,求Tn