已知函数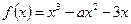
(1)若 在区间[1,+∞)上是增函数,求实数a的取值范围;
在区间[1,+∞)上是增函数,求实数a的取值范围;
(2)若x=-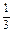 是
是 的极值点,求
的极值点,求 在[1,a]上的最大值;
在[1,a]上的最大值;
(3)在(2)的条件下,是否存在实数b,使得函数 =bx的图象与函数
=bx的图象与函数 的图象恰有3个交点,若存在,请求出实数b的取值范围;若不存在,试说明理由.
的图象恰有3个交点,若存在,请求出实数b的取值范围;若不存在,试说明理由.
【2015高考上海,文19】如图,圆锥的顶点为 ,底面的一条直径为
,底面的一条直径为 ,
, 为半圆弧
为半圆弧 的中点,
的中点, 为劣弧
为劣弧 的中点.已知
的中点.已知 ,
,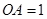 ,求三棱锥
,求三棱锥 的体积,并求异面直线
的体积,并求异面直线 与
与 所成角的大小.
所成角的大小.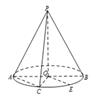
【2015高考重庆,文20】如图,三棱锥P-ABC中,平面PAC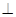 平面ABC,
平面ABC, ABC=
ABC= ,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF//BC.
,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF//BC.
(Ⅰ)证明:AB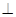 平面PFE.
平面PFE.
(Ⅱ)若四棱锥P-DFBC的体积为7,求线段BC的长.
【2015高考浙江,文18】如图,在三棱锥 中,
中, 在底面ABC的射影为BC的中点,D为
在底面ABC的射影为BC的中点,D为 的中点.
的中点.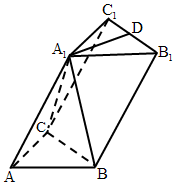
(1)证明: ;
;
(2)求直线 和平面
和平面 所成的角的正弦值.
所成的角的正弦值.
【2015高考新课标1,文18】(本小题满分12分)如图四边形ABCD为菱形,G为AC与BD交点, ,
,
(Ⅰ)证明:平面 平面
平面 ;
;
(Ⅱ)若 ,
, 三棱锥
三棱锥 的体积为
的体积为 ,求该三棱锥的侧面积.
,求该三棱锥的侧面积.
【2015高考四川,文18】一个正方体的平面展开图及该正方体的直观图的示意图如图所示.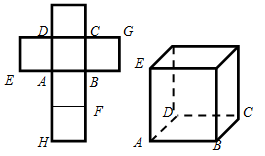
(Ⅰ)请按字母F,G,H标记在正方体相应地顶点处(不需要说明理由)
(Ⅱ)判断平面BEG与平面ACH的位置关系.并说明你的结论.
(Ⅲ)证明:直线DF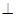 平面BEG
平面BEG