(每小题5分,满分15分)
(1)已知如下程序框图,则输出的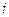 值是____________
值是____________
(2)该程序框图的功能是_________________________________

(3).按下列程序框图运算:规定:程序运行到“判断结果是否大于244”为1次运算,若x=5,则运算进行___________次才停止。
(4)给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推. 要求计算这50个数的和.将下面给出的程序框图补充完整 (1)________________________
(2)________________________ 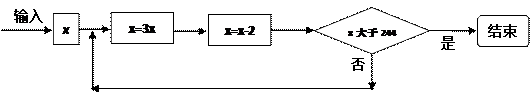
(本小题满分14分)对于函数 ,若存在
,若存在 ,使
,使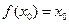 成立,则称
成立,则称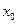 为
为 的不动点。如果函数
的不动点。如果函数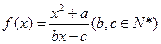 有且仅有两个不动点
有且仅有两个不动点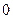 、
、 ,且
,且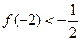 。
。
(1)试求函数 的单调区间;
的单调区间;
(2)已知各项均为负的数列 满足
满足 ,求证:
,求证: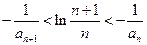 ;
;
(3)设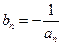 ,
,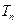 为数列
为数列 的前
的前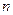 项和,求证:
项和,求证: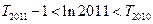 。
。
(本小题满分13分)
已知二次函数 ,直线
,直线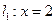 ,直线
,直线
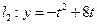 (其中
(其中 ,
,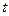 为常数);.若直线
为常数);.若直线 1、
1、 2与函数
2与函数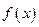 的图象以及
的图象以及 、
、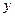 轴与函数
轴与函数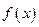 的图象所围成的封闭图形如图阴影所示.
的图象所围成的封闭图形如图阴影所示.
(Ⅰ)求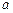 、
、 、
、 的值;
的值;
(Ⅱ)求阴影面积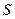 关于
关于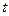 的函数
的函数 的解析式;
的解析式;
(Ⅲ)若 问是否存在实数
问是否存在实数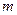 ,使得
,使得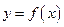 的图象与
的图象与 的图象有且只有两个不同的交点?若存在,求出
的图象有且只有两个不同的交点?若存在,求出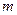 的值;若不存在,说明理由.
的值;若不存在,说明理由.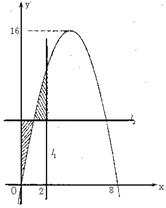
(本小题满分12分)已知△ABC的面积S满足 , 且
, 且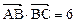 ,
,  与
与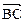 的夹角为
的夹角为 .
.
(I) 求 的取值范围;
的取值范围;
(II)求函数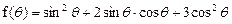 的最小值.
的最小值.
(本小题满分12分)已知函数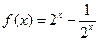 .
.
(1)若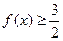 ,求x的取值范围;
,求x的取值范围;
(2)若 对于
对于 ∈[1,2]恒成立,求实数m的取值范围.
∈[1,2]恒成立,求实数m的取值范围.
(本小题满分12分)一出租车司机从某饭店到火车站途中有六个交通岗,假设他在各交通岗遇到红灯这一事件是相互独立的,并且概率都是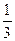 .
.
(1)求这位司机遇到红灯前,已经通过了两个交通岗的概率;
(2)求这位司机遇到红灯数 的期望与方差.
的期望与方差.