已知 中,
中, ,
, ,
, 成等差数列,求点
成等差数列,求点 的轨迹。
的轨迹。
在一次数学统考后,某班随机抽取10名同学的成绩进行样本分析,获得成绩数据的茎叶图如下.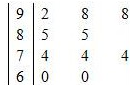
(Ⅰ)计算样本的平均成绩及方差;
(Ⅱ)现从80分以上的样本中随机抽出2名学生,求抽出的2名学生的成绩分别在 、
、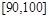 上的概率.
上的概率.
已知函数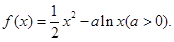
(Ⅰ)若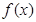 在
在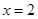 处的切线与直线
处的切线与直线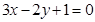 平行,求
平行,求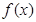 的单调区间;
的单调区间;
(Ⅱ)求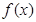 在区间
在区间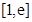 上的最小值.
上的最小值.
某公司欲招聘员工,从1000名报名者中筛选200名参加笔试,按笔试成绩择优取50名面试,再从面试对象中聘用20名员工.
(Ⅰ)求每个报名者能被聘用的概率;
(Ⅱ)随机调查了24名笔试者的成绩如下表所示:
| 分数段 |
[60,65) |
[65,70) |
[70,75) |
[75,80) |
[80,85) |
[85,90) |
| 人数 |
1 |
2 |
6 |
9 |
5 |
1 |
请你预测面试的分数线大约是多少?
(Ⅲ)公司从聘用的四男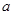 、
、 、
、 、
、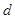 和二女
和二女 、
、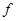 中选派两人参加某项培训,则选派结果为一男一女的概率是多少?
中选派两人参加某项培训,则选派结果为一男一女的概率是多少?
已知椭圆 抛物线
抛物线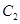 的焦点均在
的焦点均在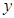 轴上,
轴上,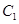 的中心和
的中心和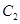 的顶点均为坐标原点
的顶点均为坐标原点 从每条曲线上取两个点,将其坐标记录于下表中:
从每条曲线上取两个点,将其坐标记录于下表中:
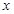 |
 |
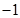 |
 |
 |
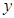 |
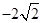 |
 |
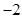 |
 |
(Ⅰ)求分别适合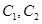 的方程的点的坐标;
的方程的点的坐标;
(Ⅱ)求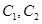 的标准方程.
的标准方程.
在三棱锥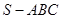 中,
中, 是边长为
是边长为 的正三角形,平面
的正三角形,平面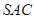 ⊥平面
⊥平面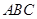 ,
, ,
, 、
、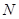 分别为
分别为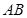 、
、 的中点.
的中点.
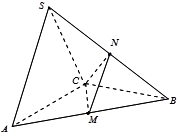
(Ⅰ)证明: ⊥
⊥ ;
;
(Ⅱ)求三棱锥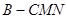 的体积.
的体积.