设函数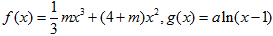 ,其中
,其中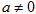 .
.
(1)若函数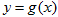 图象恒过定点P,且点P关于直线
图象恒过定点P,且点P关于直线 的对称点在
的对称点在 的图象上,求m的值;
的图象上,求m的值;
(2)当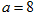 时,设
时,设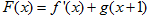 ,讨论
,讨论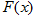 的单调性;
的单调性;
(3)在(1)的条件下,设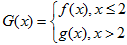 ,曲线
,曲线 上是否存在两点P、Q,使△OPQ(O为原
上是否存在两点P、Q,使△OPQ(O为原
点)是以O为直角顶点的直角三角形,且斜边的中点在y轴上?如果存在,求a的取值范围;如果不存在,
说明理由.
已知椭圆C: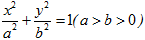 的离心率与等轴双曲线的离心率互为倒数关系,直线
的离心率与等轴双曲线的离心率互为倒数关系,直线 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切.
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切.
(1)求椭圆C的方程;
(2)设M是椭圆的上顶点,过点M分别作直线MA、MB交椭圆于A、B两点,设两直线的斜率分别为k1、k2,且k1+k2=4,证明:直线AB过定点(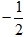 ,-l).
,-l).
已知过抛物线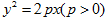 的焦点,斜率为
的焦点,斜率为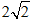 的直线交抛物线于
的直线交抛物线于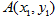 ,
,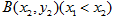 两点,且
两点,且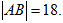
(1)求该抛物线的方程;
(2)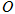 为坐标原点,
为坐标原点, 为抛物线上一点,若
为抛物线上一点,若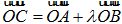 ,求
,求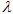 的值.
的值.
等差数列{an}的各项均为正数,a1=3,前n项和为Sn,{bn}为等比数列,b1=1,且b2S2=64,b3S3=960.
(1)求an与bn;
(2)求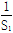 +
+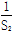 +…+
+…+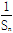 .
.
已知函数 在区间
在区间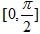 上的最大值为2.
上的最大值为2.
(1)求常数m的值;
(2)在△ABC中,角A、B、C所对的边是a、b、c,若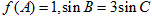 ,△ABC面积为
,△ABC面积为 .求边长a.
.求边长a.