设函数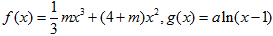 ,其中
,其中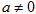 .
.
(1)若函数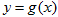 图象恒过定点P,且点P关于直线
图象恒过定点P,且点P关于直线 的对称点在
的对称点在 的图象上,求m的值;
的图象上,求m的值;
(2)当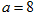 时,设
时,设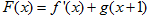 ,讨论
,讨论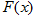 的单调性;
的单调性;
(3)在(1)的条件下,设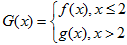 ,曲线
,曲线 上是否存在两点P、Q,使△OPQ(O为原
上是否存在两点P、Q,使△OPQ(O为原
点)是以O为直角顶点的直角三角形,且斜边的中点在y轴上?如果存在,求a的取值范围;如果不存在,
说明理由.
(本小题满分12分)已知高二年级的某6名学生,独立回答某类问题时答对的概率都是0.5,而将这6名同学平均分成3个小组后,每个小组经过两名同学讨论后再回答同类问题时答对此类问题的概率都是0.7,若各个同学或各个小组回答问题时都是相互独立的.
(Ⅰ)这6名同学平均分成3组,共有分法多少种?
(Ⅱ)若已经平均分成了甲、乙、丙3个小组,则3个小组中恰有2组能答对此类问题的概率是多少?
(Ⅲ)若要求独立回答,则这6名学生中至多有4人能答对此类问题的概率是多少?
(本小题满分12分)已知 的展开式中常数项为1120.
的展开式中常数项为1120.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)求二项展开式中含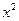 的项.
的项.
(本小题满分12分)设 是一个离散型随机变量,其分布列如下表,试求随机变量
是一个离散型随机变量,其分布列如下表,试求随机变量 的期望
的期望 与方差
与方差 .
.
| ξ |
-1 |
0 |
1 |
| P |
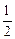 |
1-2q |
q2 |
(本小题满分14分)设函数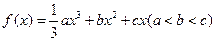 ,其图象对应的曲线设为G.(Ⅰ)设
,其图象对应的曲线设为G.(Ⅰ)设 、
、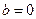 、
、 ,
, 为经过点(2,2)的曲线G的切线,求
为经过点(2,2)的曲线G的切线,求 的方程;
的方程;
(Ⅱ)已知曲线G在点A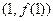 、B
、B 处的切线的斜率分别为0、
处的切线的斜率分别为0、 ,求证:
,求证: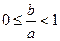 ;
;
(Ⅲ)在(Ⅱ)的条件下,当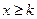 时,
时, 恒成立,求常数
恒成立,求常数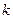 的最小值.
的最小值.
(本小题满分12分)已知
 ,设
,设 ,
,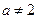 .(Ⅰ)求出函数
.(Ⅰ)求出函数 的解析式;(Ⅱ)是否存在
的解析式;(Ⅱ)是否存在 使得函数
使得函数 能以
能以 为其最小值?若能,求出对应的
为其最小值?若能,求出对应的 的取值或取值范围;若不能,试说明理由.
的取值或取值范围;若不能,试说明理由.