若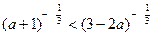
，试求
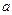的取值范围.
（本小题满分12分）科研所研究人员都具有本科和研究生两类学历,年龄段和学历如下表,从该科研所任选一名研究人员,是本科生概率是
,是35岁以下的研究生概率是
.
（Ⅰ）求出表格中的
和
的值;
（Ⅱ）设“从数学教研组任选两名教师,本科一名,研究生一名,50岁以上本科生和35岁以下的研究生不全选中” 的事件为A,求事件A概率P(A).
（本小题满分12分）
如图，已知棱柱
的底面是菱形，且
面
，
，
=１，
为棱
的中点，
为线段
的中点．
（Ⅰ）求证：
面；
（Ⅱ）试判断直线ＭＦ与平面
的位置关系，并证明你的结论；
（Ⅲ）求三棱锥
的体积．
（本小题满分12分）
已知向量：
，
，函数
.
（1）求函数
的最小正周期和单调递增区间；
（2）求
的对称轴并作出在
的图象．
（本小题满分13分）已知数列
中，
，
．
（Ⅰ）若
，设
，求证数列
是等比数列，并求出数列的通项公式；
（Ⅱ）若
，
，
，证明：
．
（本小题满分13分）已知椭圆
（
）的离心率为
，且短轴长为2．
（Ⅰ）求椭圆的方程；
（Ⅱ）若与两坐标轴都不垂直的直线
与椭圆交于
两点，
为坐标原点，且
，
，求直线的方程．