(本小题满分13分)已知椭圆 (
( )的离心率为
)的离心率为 ,且短轴长为2.
,且短轴长为2.
(Ⅰ)求椭圆的方程;
(Ⅱ)若与两坐标轴都不垂直的直线 与椭圆交于
与椭圆交于 两点,
两点, 为坐标原点,且
为坐标原点,且 ,
, ,求直线
,求直线 的方程.
的方程.
(满分12分)渔船甲位于岛屿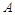 的南偏西
的南偏西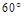 方向
方向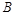 处,且与岛屿
处,且与岛屿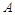 相距
相距 海里,渔船乙以
海里,渔船乙以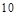 海里/小时的速度从岛屿
海里/小时的速度从岛屿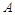 出发沿正北方向航行,若渔船甲同时从
出发沿正北方向航行,若渔船甲同时从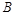 处出发沿北偏东
处出发沿北偏东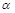 的方向追赶渔船乙,刚好用了2小时追赶上渔船乙.
的方向追赶渔船乙,刚好用了2小时追赶上渔船乙.
(Ⅰ)求渔船甲的速度;
(Ⅱ)求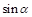 的值.
的值.
(满分14分)已知函数 .
.
(Ⅰ)若曲线 在
在 和
和 处的切线互相平行,求
处的切线互相平行,求 的值;
的值;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)设 ,若对任意
,若对任意 ,均存在
,均存在 ,使得
,使得 ,求
,求 的取值范围.
的取值范围.
(满分13分)设函数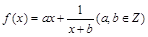 ,曲线
,曲线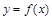 在点
在点 处的切线方程是
处的切线方程是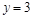
(Ⅰ)求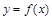 的解析式;
的解析式;
(Ⅱ)证明:函数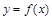 的图象是一个中心对称图形,并求其对称中心;
的图象是一个中心对称图形,并求其对称中心;
(Ⅲ)证明:曲线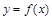 上任意一点的切线与直线
上任意一点的切线与直线 和直线
和直线 所围成的三角形的面积是定值,并求出这个定值.
所围成的三角形的面积是定值,并求出这个定值.
(满分12分)已知向量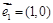 ,
, ,动点
,动点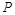 从点
从点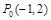 开始沿着与向量
开始沿着与向量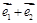 相同的方向做匀速直线运动,速度大小为
相同的方向做匀速直线运动,速度大小为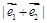 ;另一动点
;另一动点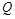 从点
从点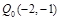 开始沿着与向量
开始沿着与向量 相同的方向做匀速直线运动,速度大小为
相同的方向做匀速直线运动,速度大小为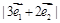 ,设
,设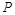 、
、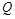 在
在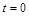 秒时刻分别在
秒时刻分别在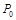 、
、 处.
处.
(Ⅰ)经过多长时间 最小?求出最小值;
最小?求出最小值;
(Ⅱ)经过多长时间后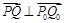 ,求出
,求出 值.
值.
(满分12分)已知函数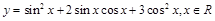
(Ⅰ)求函数的最小正周期;
(Ⅱ)求函数的单调增区间.