已知集合M是满足下列性质的函数 的全体:若存在非零常数k,对任意
的全体:若存在非零常数k,对任意 ,等式
,等式 恒成立。
恒成立。
(Ⅰ)判断一次函数 是否属于集合M;
是否属于集合M;
(Ⅱ)证明 属于集合M,并找到一个常数k;
属于集合M,并找到一个常数k;
(Ⅲ)已知函数 与
与 的图像有公共点,试证明
的图像有公共点,试证明
(本小题满分13分)
已知椭圆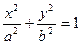 (
(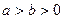 )的右焦点为
)的右焦点为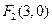 ,离心率为
,离心率为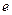 .
.
(Ⅰ)若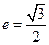 ,求椭圆的方程;
,求椭圆的方程;
(Ⅱ)设直线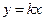 与椭圆相交于
与椭圆相交于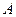 ,
,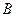 两点,
两点,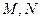 分别为线段
分别为线段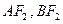 的中点. 若坐标原点
的中点. 若坐标原点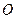 在以
在以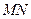 为直径的圆上,且
为直径的圆上,且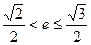 ,求
,求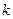 的取值范围.
的取值范围.
(本小题满分13分)
一个袋中装有 个形状大小完全相同的小球,球的编号分别为
个形状大小完全相同的小球,球的编号分别为 .
.
(Ⅰ)若从袋中每次随机抽取1个球,有放回的抽取2次,求取出的两个球编号之和为6的概率;
(Ⅱ)若从袋中每次随机抽取 个球,有放回的抽取3次,求恰有
个球,有放回的抽取3次,求恰有 次抽到
次抽到 号球的概率;
号球的概率;
(Ⅲ)若一次从袋中随机抽取 个球,记球的最大编号为
个球,记球的最大编号为 ,求随机变量
,求随机变量 的分布列.
的分布列.
(本小题满分13分)
如图,在三棱柱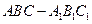 中,侧面
中,侧面 ,
,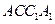 均为正方形,∠
均为正方形,∠ ,点
,点 是棱
是棱 的中点.
的中点.
(Ⅰ)求证: ⊥平面
⊥平面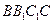 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求二面角 的余弦值.
的余弦值.
(本小题满分13分)
已知函数 .
.
(Ⅰ)若点 在角
在角 的终边上,求
的终边上,求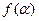 的值;
的值;
(Ⅱ)若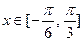 ,求
,求 的值域.
的值域.
已知函数 (
( ,
, ,
,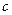 为常数,
为常数, ).
).
(Ⅰ)若 时,数列
时,数列 满足条件:点
满足条件:点 在函数
在函数 的图象上,求
的图象上,求 的前
的前 项和
项和 ;
;
(Ⅱ)在(Ⅰ)的条件下,若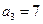 ,
, ,
, (
( ),
),
证明: ;
;
(Ⅲ)若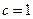 时,
时,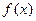 是奇函数,
是奇函数, ,数列
,数列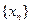 满足
满足 ,
,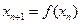 ,
,
求证: .
.