(本小题满分13分)
如图,在三棱柱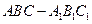 中,侧面
中,侧面 ,
,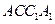 均为正方形,∠
均为正方形,∠ ,点
,点 是棱
是棱 的中点.
的中点.
(Ⅰ)求证: ⊥平面
⊥平面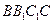 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求二面角 的余弦值.
的余弦值.
设数列 是等差数列,且
是等差数列,且 且
且 成等比数列。
成等比数列。
(1).求数列 的通项公式
的通项公式
(2).设 ,求前n项和
,求前n项和 .
.
已知f(x)=|x+1|+|x-1|,不等式f(x)的解集为M.
(1)求M;
(2)当a,b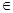 M时,证明:2|a+b|<|4+ab|.
M时,证明:2|a+b|<|4+ab|.
以直角坐标系的原点为极点O,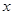 轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为
轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为 ,若直线l经过点P,且倾斜角为
,若直线l经过点P,且倾斜角为 ,圆C的半径为4.
,圆C的半径为4.
(1).求直线l的参数方程及圆C的极坐标方程;
(2).试判断直线l与圆C有位置关系.
如图,四边形为边长为a的正方形,以D为圆心,DA为半径的圆弧与以BC为直径的圆O交于F,连接CF并延长交AB于点E.
(1).求证:E为AB的中点;
(2).求线段FB的长.
已知函数 ,
,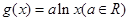 .
.
(1)a≥-2时,求F(x)=f(x)-g(x)的单调区间;
(2)设h(x)=f(x)+g(x),且h(x)有两个极值点为 ,其中
,其中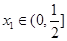 ,求
,求 的最小值.
的最小值.