设函数 .
.
(1)当 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程;
(2)当 时,
时, 的最大值为
的最大值为 ,求
,求 的取值范围.
的取值范围.
如图,△ABC是直角三角形,∠ACB=90°,CD⊥AB于D,E是AC的中点,ED的延长线与CB的延长线交于点F.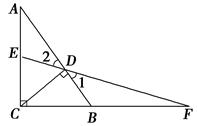
求证:FD2=FB·FC.
如图,在△ABC中,延长BC到D,使CD=BC,取AB的中点F,连接FD交AC于点E.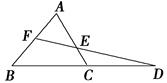
(1)求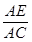 的值;
的值;
(2)若AB=a,FB=EC,求AC的长.
如图所示,在△ABC中,AE∶EB=1∶3,BD∶DC=2∶1,AD与CE相交于F,求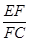 +
+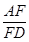 的值.
的值.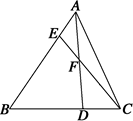
已知AD是△ABC的内角平分线,求证: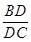 =
= .
.
如图所示,已知平面α∥平面β,点P是平面α、β外一点,且直线PB分别与α、β相交于A、B,直线PD分别与α、β相交于C、D.
(1)求证:AC∥BD;
(2)如果PA=4 cm,AB=5 cm,PC=3 cm,求PD的长.