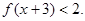(已知二次函数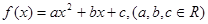 满足:对任意实数x,都有
满足:对任意实数x,都有 ,且当
,且当 (1,3)时,有
(1,3)时,有 成立。
成立。
(1)证明: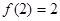 ;
;
(2)若 的表达式;
的表达式;
(3)在(2)的条件下,设 ,
, ,若
,若 图上的点都位于直线
图上的点都位于直线 的上方,求实数m的取值范围。
的上方,求实数m的取值范围。
(某公司租地建仓库,每月土地占用费y1与车库到车站的距离成反比,而每月库存货物的运费y2与到车站的距离成正比,如果在距车站10公里处建仓库,这两项费用y1和y2分别为2万元和8万元,那么要使这两项费用之和最小,仓库应建在离车站多少公里处?
(已知抛物线y=x2+1,定点A(3,1)、B为抛物线上任意一点,点P在线段AB上,且有BP∶PA=1∶2,当B点在抛物线上变动时,求点P的轨迹方程.
某企业生产A、B两种产品,生产每一吨产品所需的劳动力、煤和电耗如下表:
已知生产每吨A产品的利润是7万元,生产每吨B产品的利润是12万元,现因条件限制,该企业仅有劳动力300个,煤360吨,并且供电局只能供电200千瓦,试问该企业生产A、B两种产品各多少吨,才能获得最大利润?
| 产品品种 |
劳动力(个) |
煤(吨) |
电(千瓦) |
| A产品 |
3 |
9 |
4 |
| B产品 |
10 |
4 |
5 |
若f(x)是定义在(0,+∞)上的增函数,且对一切x>0满足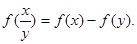
(1)求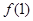 的值; (2)若
的值; (2)若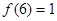 ,解不等式
,解不等式