(本小题满分14分)设甲、乙两套试验方案在一次试验中成功的概率均为p,且这两套试验方案中至少有一套试验成功的概率为0.51,假设这两套试验方案在试验过程中,相互之间没有影响.,设试验成功的方案的个数为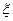 .(Ⅰ)求p的值;(Ⅱ)求
.(Ⅰ)求p的值;(Ⅱ)求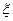 的数学期望E
的数学期望E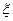 与方差D
与方差D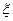 .
.
已知向量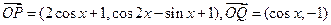 ,定义
,定义 .
.
(1)求函数 的单调递减区间;
的单调递减区间;
(2)求函数 的最大值及取得最大值时的
的最大值及取得最大值时的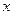 的取值集合.
的取值集合.
已知函数
(1)求函数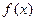 的最小正周期;
的最小正周期;
(2)若对任意的x∈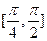 ,不等式f(x)>m-3恒成立,求实数m的取值范围.
,不等式f(x)>m-3恒成立,求实数m的取值范围.
在三角形ABC中,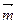 =(cos
=(cos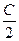 ,sin
,sin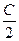 ),
), 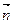 =(cos
=(cos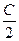 ,-sin
,-sin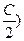 且
且 的夹角为
的夹角为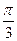
(1)求C;
(2)已知c=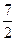 ,三角形的面积S=
,三角形的面积S=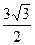 ,求a+b(a、b、c分别∠A、∠B、∠C所对的边)
,求a+b(a、b、c分别∠A、∠B、∠C所对的边)
在△ABC中,A、B、C的对边分别是a、b、c,且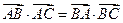
(1)判断△ABC的形状;
(2)若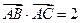 ,求边c的值.
,求边c的值.
某单位在抗雪救灾中,需要在A、B两地之间架设高压电线,测量人员在相距6000m的C、D两地(A、B、C、D在同一平面上),测得∠ACD=45°,∠ADC=75°,∠BCD=30°,∠BDC=15°(如图),假如考虑到电线的自然下垂和施工损耗等原因,实际所须电线长度大约应该是A、B距离的1.2倍,问施工单位至少应该准备多长的电线?(参考数据: )
)