如图,已知斜三棱柱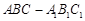 ,
, ,
, ,
, 在底面
在底面 上的射影恰为
上的射影恰为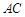 的中点
的中点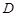 , 又知
, 又知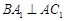 .
.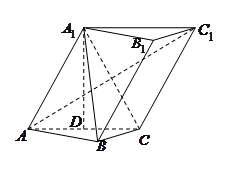
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求 到平面
到平面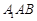 的距离;
的距离;
(Ⅲ)求二面角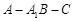 的平面角的余弦值.
的平面角的余弦值.
已知空间四边形ABCD中,AB⊥CD,AC⊥BD,证明AD⊥BC。
已知双曲线 和椭圆
和椭圆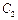 有相同的焦点
有相同的焦点 和
和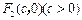 ,两曲线在第一象限内的交点为
,两曲线在第一象限内的交点为 ,椭圆
,椭圆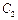 与
与 轴负半轴交于点
轴负半轴交于点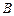 ,且
,且 三点共线,
三点共线, 分有向线段
分有向线段 的比为
的比为 ,又直线
,又直线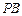 与双曲线
与双曲线 的另一交点为
的另一交点为 ,若
,若 .
.
(1)求椭圆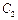 的离心率;
的离心率;
(2)求双曲线 和椭圆
和椭圆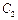 的方程.
的方程.
如图,平面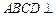 平面
平面 是正方形,
是正方形,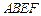 是矩形,且
是矩形,且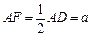 ,
,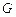 是
是 的中点.
的中点.
(1)求 与平面
与平面 所成角
所成角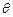 的正弦值;
的正弦值;
(2)求二面角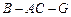 的余弦值.
的余弦值.
已知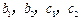 均为实数,命题
均为实数,命题 方程
方程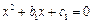 无实根;命题
无实根;命题 无实根.判断当
无实根.判断当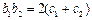 时,命题
时,命题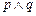 的真假.
的真假.
已知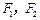 是椭圆
是椭圆 的左、右焦点,
的左、右焦点,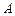 是椭圆上位于第一象限内的一点,点
是椭圆上位于第一象限内的一点,点 也在椭圆上,且满足
也在椭圆上,且满足 (
(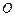 为坐标原点),
为坐标原点),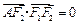 .若椭圆的离心率等于
.若椭圆的离心率等于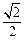 .
.
(1)求直线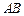 的方程;
的方程;
(2)若三角形 的面积等于
的面积等于 ,求椭圆的方程.
,求椭圆的方程.