（本小题满分12分）
定义在
上的增函数
对任意
都有
。
（1）求
；
（2）求证：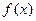
为奇函数；
（3）若
对任意
恒成立，求实数
的取值范围。
已知双曲线与椭圆可
共焦点，它们的离心率之和为
，求双曲线方程。
已知ΔABC的三条边分别为
求证：
某企业为考察生产同一种产品的甲、乙两条生产线的产品合格率，同时各抽取100件产品，检验后得到如下联表：
生产线与产品合格率列联表
| 合格 |
不合格 |
总计 |
|
| 甲线 |
97 |
3 |
100 |
| 乙线 |
95 |
5 |
100 |
| 总计 |
192 |
8 |
200 |
请问甲、乙两线生产的产品合格率在多大程度上有关系？(本题满分10分)
附：
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
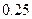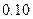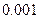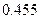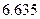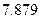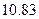(本小题满分12分)
函数
)
（Ⅰ）已知
的展开式中
的系数为
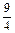，求常数
（Ⅱ）已知
,是否存在
的值,使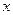
在定义域中取任意值时，
恒成立？如存在，求出的值，如不存在，说明理由.
(本小题满分12分)
一个袋子内装有若干个黑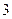球，
个白球，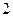
个红球（所有的球除颜色外其它均相同），从中任取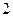个球，每取得一个黑球得
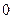分，每取一个白球得
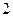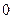分，每取一个红球得分，已知得分的概率为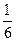
，用随机变量X表示取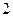个球的总得分.
（Ⅰ）求袋子内黑球的个数；
（Ⅱ）求X的分布列.