在进行一项掷骰子放球游戏中,规定:若掷出1点,甲盒中放一球;若掷出2点或3点,乙盒中放一球;若掷出4点或5点或6点,丙盒中放一球,前后共掷3次,设 分别表示甲,乙,丙3个盒中的球数.
分别表示甲,乙,丙3个盒中的球数.
(Ⅰ)求 依次成公差大于0的等差数列的概率;
依次成公差大于0的等差数列的概率;
(Ⅱ)求随机变量z的概率分布列和数学期望.
(本小题满分12分)等差数列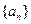 的前
的前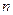 项和为
项和为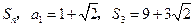 .
.
⑴求数列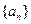 的通项
的通项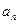 与前
与前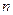 项和
项和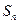 ;⑵设
;⑵设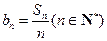 ,求证:数列
,求证:数列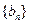 中任意不同的三项都不可能成为等比数列.
中任意不同的三项都不可能成为等比数列.
(本小题满分12分)在四边形ABCD中, BD是它的一条对角线,且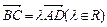 ,
,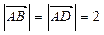 ,
, .⑴若△BCD是直角三形,求
.⑴若△BCD是直角三形,求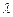 的值;⑵在⑴的条件下,求
的值;⑵在⑴的条件下,求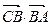 .
.
(本小题满分12分)
如图,在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
⑴证明PA//平面EDB; ⑵证明PB⊥平面EFD;
⑵证明PB⊥平面EFD;
⑶求二面角C—PB—D的大小.
已知函数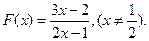

(1)求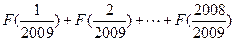 的值;
的值;
(2)已知数列 ,求数列
,求数列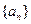 的通项公式;
的通项公式;
(3)求证: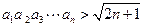 .
.
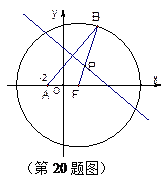
已知定点A(-2,0),动点B是圆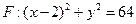 (F为圆心)上一点,线段AB的垂直平分线交BF于P.
(F为圆心)上一点,线段AB的垂直平分线交BF于P.
(1)求动点P的轨迹方程;
(2)是否存在过点E(0,-4)的直线l交P点的轨迹于点R,T,且满足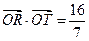 (O为原点).若存在,求直线l的方程;若不存在,请说明理由.
(O为原点).若存在,求直线l的方程;若不存在,请说明理由.