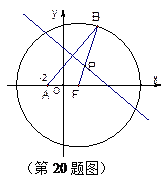
已知定点A(-2,0),动点B是圆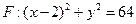 (F为圆心)上一点,线段AB的垂直平分线交BF于P.
(F为圆心)上一点,线段AB的垂直平分线交BF于P.
(1)求动点P的轨迹方程;
(2)是否存在过点E(0,-4)的直线l交P点的轨迹于点R,T, 且满足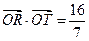 (O为原点).若存在,求直线l的方程;若不存在,请说明理由.
(O为原点).若存在,求直线l的方程;若不存在,请说明理由.
(本小题满分13分)
已知正项数列{an}的首项a1=,函数f(x)=,g(x)=.
(1)若正项数列{an}满足an+1=f(an)(n∈N*),证明:{}是等差数列,并求数列{an}的通项公式;
(2)若正项数列{an}满足an+1≤f(an)(n∈N*),数列{bn}满足bn=,证明:b1+b2+…+bn<1;
(3)若正项数列{an}满足an+1=g(an),求证:|an+1-an|≤·()n-1
(本小题满分13分)
某旅游景区的观景台P位于高(山顶到山脚水平面M的垂直高度PO)为2km的山峰上,山脚下有一段位于水平线上笔直的公路AB,山坡面可近似地看作平面PAB,且△PAB为等腰三角形.山坡面与山脚所在水平面M所成的二面角为α(0°<α<90°),且sinα=.现从山脚的水平公路AB某处C0开始修建一条盘山公路,该公路的第一段、第二段、第三段…,第n-1段依次为C0C1,C1C2,C2C3,…,Cn-1Cn(如图所示),且C0C1,C1C2,C2C3,…,Cn-1Cn与AB所成的角均为β,其中0<β<90°,sinβ=.试问: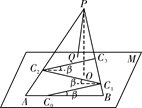
(1)每修建盘山公路多少米,垂直高度就能升高100米.若修建盘山公路至半山腰(高度为山高的一半),在半山腰的中心Q处修建上山缆车索道站,索道PQ依山而建(与山坡面平行,离坡面高度忽略不计),问盘山公路的长度和索道的长度各是多少?
(2)若修建xkm盘山公路,其造价为 a万元.修建索道的造价为2a万元/km.问修建盘山公路至多高时,再修建上山索道至观景台,总造价最少.
(本小题满分13分)
已知函数f(x)=-x2+ax-lnx(a∈R).
(1)求函数f(x)既有极大值又有极小值的充要条件;
(2)当函数f(x)在[,2]上单调时,求a的取值范围.
(本小题满分12分)
如图,在体积为1的三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥AC,AC=AA1=1,P为线段AB上的动点.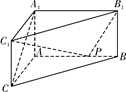
(1)求证:CA1⊥C1P;
(2)当AP为何值时,二面角C1-PB1-A1的大小为?
(本小题满分12分)
在高三年级某班组织的欢庆元旦活动中,有一项游戏规则如下:参与者最多有5次抽题并答题的机会.如果累计答对2道题,立即结束游戏,并获得纪念品;如果5次机会用完仍未累计答对2道题,也结束游戏,并不能获得纪念品.已知某参与者答对每道题答对的概率都是,且每道题答对与否互不影响.
(1)求该参与者获得纪念品的概率;
(2)记该参与者游戏时答题的个数为 ,求
,求 的分布列及期望
的分布列及期望